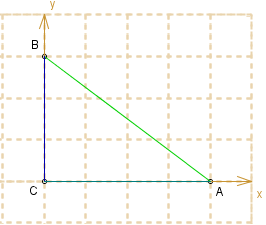
Urok trójkąta 3, 4, 5 jest niesamowity:
Każdy belfer docenia jego walory;
wiele zadań o nim ma 'zgrabne odpowiedzi'
(będące liczbami całkowitymi),
na przykład:
- pole = . . . . . ,
- obwód = . . . . . ,
- promień okręgu wpisanego = . . . . . .
Odpowiednikiem trójkąta w przestrzeni jest czworościan.
Spróbujemy znaleźć
i ścianach będących trójkątami prostokątnymi.
Spróbujemy znaleźć uroczy czworościan.
(Rozważania będą dość trudne choć całkiem elementarne.)
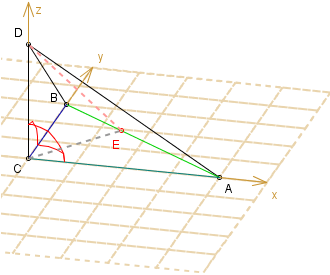Rozważmy na początek czworościan ABCD taki, że w wierzchołku C
ściany mają kąty proste, tzn.
ACB
= ACD
= BCD = 90o.
Gdy CE jest wysokością trójkąta ABC,
to DE jest wysokością trójkąta ABD
(pomyśl o płaszczyźnie CED - jest prostopadła do AB).
Zatem kąty EAD i EBD są ostre.
Kąt ADB też jest ostry (można powtórzyć powyższe rozumowanie dla wysokości CF ściany CBD).
Zatem trójkąt ABD jest ostrokątny (można to też uzasadnić korzystając z tw. Pitagorasa).
Wniosek 1. Jeśli w czworościanie w jednym z wierzchołków wszystkie ściany mają kąty proste, to ściana przeciwległa do tego wierzchołka jest trójkątem ostrokątnym.
Wniosek 2. Nie istnieje uroczy czworościan, w którym w jednym z wierzchołków wszystkie ściany mają kąty proste.
Może można zbudować uroczy czworościan
z samych trójkątów 3,4,5?
Zbadamy to.
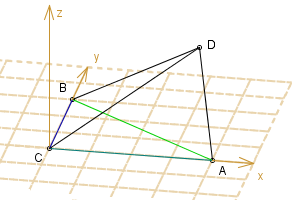
Gdyby w podstawie ABC było:
BD = 4 (nie może być =3, bo . . . . . ,
nie może być =5, bo . . . . . ),
CD = 5 (nie może być =3, bo . . . . . ,
nie może być =4, bo . . . . . ),
AD = 3 (nie może być =4, bo . . . . . ,
nie może być =5, bo . . . . . ).
Zatem kątami prostymi byłyby: CBD i CAD. Zobacz
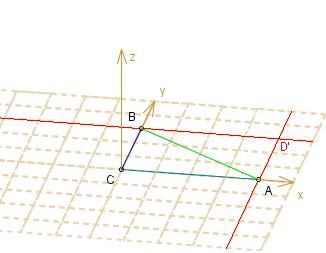Gdyby kąt CBD był prosty,
to punkt D leżałby gdzieś nad/pod prostą BD'.
Gdyby kąt CAD był prosty, to punkt D leżałby gdzieś nad/pod prostą AD'.
Zatem D leżałby nad/pod punktem D'.
Jednak wtedy trójkąt ABD nie byłby prostokątny (dlaczego?).
(Dokładniej: punkt D musiałby leżeć na przecięciu
okręgów zaznaczonych na rysunku
.)
Z powyższych rozważań wynika:
Wniosek 3. Nie istnieje uroczy czworościan o ścianach 3,4,5.
Jeśli dokładnie prześledzisz powyższe rozumowanie, to zobaczysz:
Wniosek 4. Nie istnieje czworościan ABCD, w którym kąty: ACB, CBD, CAD byłyby proste i ściana ABD byłaby trójkątem prostokątnym.
Dotychczasowe fiasko poszukiwań uroczego czworościanu może być deprymujące.
Wszystkie powyższe rozumowania pokazują (sic!), że czegoś nie ma.
Nie ma pewnych czworościanów o ścianach będących trójkątami prostokątnymi.
Może nie ma żadnych czworościanów o ścianach będących trójkątami prostokątnymi?
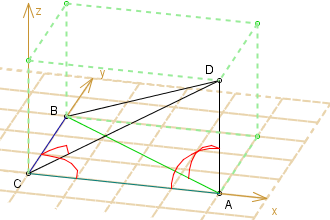
Nie jest tak źle, patrz obok.
Czworościan ABCD jest wycięty z prostopadłościanu 3×4×h. Wszystkie jego ściany są trójkątami prostokątnymi.
Czy jest on uroczy?
Czy można tak dobrać h = AD,
by wszystkie jego krawędzie były całkowite?
Niestety nie. Sprawdź:
Zauważ, że BD > CD (dlaczego?).
Ponadto różnica długości tych krawędzi jest równa
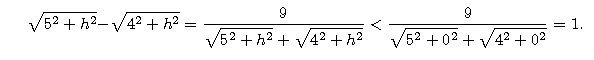Różnica mniejsza od 1 oznacza, że nie mogą to być dwie liczby całkowite!
Czas na sukces:
Czworościan wycięty (jak powyższy) z prostopadłościanu 104 × 153 × 673 jest uroczy.
Dokładniej: czworościan ABCD, w którym:
Można to sprawdzić przy pomocy twierdzenia Pitagorasa (a raczej twierdzenia odwrotnego).
Urok tego czworościanu jest niemały, oblicz:
- pole powierzchni całkowitej,
- objętość,
- promień kuli wpisanej w czworościan,
- promień kuli opisanej na czworościanie.
Są tylko dwa urocze czworościany o krawędziach długości mniejszej niż 1000.
Ten drugi ma krawędzie długości: 520, 117, 756, 533, 765, 925, dokładniej:
Jak sprawdzić, że faktycznie nie ma innych?
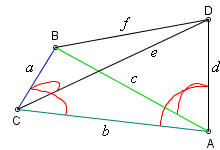Po pierwsze:
należy pokazać, że w uroczych czworościanach kąty proste ścian są rozłożone tak, jak na rysunku obok.
(Trzeba wykluczyć inne układy, podobnie jak we Wnioskach 1-4. Pomijamy tu te żmudne rozważania.)
Po drugie: należy rozwiązać w liczbach naturalnych, mniejszych od 1000 układ równań:
W efekcie dostajemy dwa (nieprzystające) czworościany opisane powyżej.