Wszystkie rysunki w tym tekście są dynamiczne,
można przesuwać 'suwaki' znajdujące się z lewej strony,
można powiększać/pomniejszać rysunki, kręcąc kółkiem myszki.
Rysunki utworzono przy użyciu programu C.a.R. - dziękujemy Rene Grothmannowi.
Pocisk (zielony stożek S o wysokości h i promieniu podstawy r)
wbił się w pniak (brązowy walec W o wysokości H i promieniu podstawy R=1).
Wbił się nie byle jak. Jak? Ano tak, że jego podstawa jest styczna do powierzchni
bocznej W i jego wysokość jest zawarta w (pewnym) promieniu podstawy W.
Jaka jest objętość V bryły odłupanej przez pocisk?
(Jaka jest objętość V części W zawartej w S ?
Jaka jest objętość V części S zawartej w W ? )
Jak to wygląda?
Jak wygląda linia, będąca wspólną częścią powierzchni W i
powierzchni S ?
Przesuwając suwak Q, zobaczysz jak skonstruować punkt Z tej linii.
Przesuwając suwak 'zobacz', zobaczysz jak wygląda ta linia.
Można, stosunkowo nietrudno, wyznaczyć równanie tej linii (jednak nie będziemy tu tego robić).
Niech P oznacza pole części powierzchni bocznej W ograniczonej tą linią.
Można zobaczyć, że
V = 1/3 . P . R
(wystarczy podzielić tę bryłę na klinki, patrz Klina klinem).
Zatem, by podać ostateczny wzór na V wystarczy wyznaczyć P (w zależności
od R, H, r, h).
I tu niespodzianka: N I E D A S I Ę !
Co to znaczy 'nie da się'? Nawet w przypadku R = H = r =h nie ma takiego wzoru na P.
Nie ma i nie będzie! Można to udowodnić! Można udowodnić, że nie ma wzoru!
Taki dowód wymaga jednak znajomości matematyki wyższej (P wyraża się przez całkę eliptyczną).
Nie ma wzoru na V, ale ta objętość istnieje! Jak ją obliczyć?
Cóż - pozostaje pogodzić się z faktem, że możemy otrzymać tylko przybliżone wartości tej wielkości.
Na zakończenie dodajmy, że podobnie jest również w poniższym przypadku:
Pocisk (zielony stożek S o wysokości h i promieniu podstawy r)
wbił się w pniak (brązowy stożek W o wysokości H i promieniu podstawy R=1).
Wbił się nie byle jak. Jak? Ano tak, że jego podstawa jest styczna do powierzchni
bocznej W i jego wysokość jest zawarta w (pewnym) promieniu podstawy W.
Jaka jest objętość V bryły odłupanej przez pocisk?
(Jaka jest objętość V części W zawartej w S ?
Jaka jest objętość V części S zawartej w W ? )
Jak to wygląda?
Jak wygląda linia, będąca wspólną częścią powierzchni W i
powierzchni S ?
Przesuwając suwak Q, zobaczysz jak skonstruować punkt Z tej linii.
Przesuwając suwak 'zobacz', zobaczysz jak wygląda ta linia.
Zobaczysz też cień (rzut) tej linii na podstawę W.
Niech P oznacza pole części powierzchni bocznej W ograniczonej tą linią
i niech P' oznacza pole części powierzchni podstawy W ograniczonej cieniem tej linii.
Można zobaczyć, że
V = 1/3 . P .
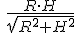 , ,
V = 1/3 . P' . H
(podobnie jak opisano w artykule Klin ze stożka).
|