|
Wszystkie rysunki w tym tekście są dynamiczne, można przesuwać <suwaki> znajdujące się z lewej strony.
Rysunki utworzono przy użyciu programu C.a.R. - dziękujemy Rene Grothmannowi.
Graniastosłup prawidłowy, o podstawie będącej n-kątem foremnym
A1A2...An, przecinamy
płaszczyzną przechodzącą pomiędzy podstawami. Otrzymujemy graniastosłup ścięty.
Niech P oznacza pole podstawy
A1A2...An
i niech hk = AkAk'.
V = P . 1/n (h1 + h2 + ... + hn) . Dla parzystych n dowód można po prostu zobaczyć (przestaw suwak <dowód> ):
Co widzisz?
Uwaga 1.
Dla n = 3 podajemy poniżej dwa dowody wzoru na objętość:
Uwaga 2.
Uwaga 3.
Uwaga 4.
Środek S n-kąta foremnego wyznacza podział podstawy na n trójkątów o równych polach. Te trójkąty wyznaczają podział graniastosłupa ściętego na n graniastosłupów ściętych o podstawach trójkątnych. Stosując dla nich wzór na objętość, dostaniemy wzór ogólny:
Uwaga 5.
- Punkt S jest środkiem ciężkości wierzchołków podstawy, czyli
- Wybierzmy tak układ współrzędnych (na podstawie), by S = (0,0). Wtedy dla współrzędnych punktów Ak = (xk,yk) mamy: - Równanie płaszczyzny tnącej jest postaci f(x,y) = ax + by + c. - Reszty dowodzi poniższy rachunek: 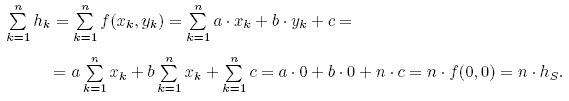
Uwaga 6.
- Jest wygodniejszy w stosowaniu - wystarczy zmierzyć jedną wielkość hn (a nie n). - Natychmiast z tego wzoru wynika, że gdy będziemy kręcić graniastosłupem prawidłowym
wzdłuż osi prostopadłej do podstawy, przechodzącej przez S, to płaszczyzna tnąca
będzie wycinała różne graniastosłupy ścięte (o różnych h1,...,hn),
ale o tej samej objętości V = P . hS .
- Trzeci powód:
Podamy tu szkic uzasadnienia. Najpierw określimy nieprecyzyjnie pojęcie środka ciężkości figury płaskiej F (dla formalnej definicji potrzebne jest pojęcie całki): -
Podzielmy figurę F o polu P na 'małe' części o polach
p1, p2,...,pm
i wybierzmy po jednym punkcie
Z1, Z2,...,Zm z każdej części.
- Wybierzmy tak układ współrzędnych (na podstawie), by środek ciężkości S = (0,0). Wtedy dla współrzędnych punktów Zi = (xi,yi) mamy: - Równanie płaszczyzny tnącej jest postaci f(x,y) = ax + by + c. - Reszty dowodzi poniższy rachunek (formalnie potrzebny tu jest drobny rachunek całkowy): 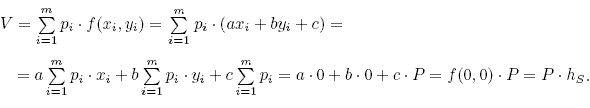
Uwaga 7.
Na deser zobaczmy, że dla brył wyciętych z graniastosłupów prawidłowych (już niekoniecznie jedną płaszczyzną), zachodzi następujący wzór:
|