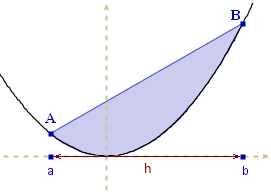
Na rysunku widać odcinek paraboli, to znaczy obszar ograniczony parabolą i cięciwą paraboli (odcinkiem o końcach leżących na paraboli).

Wyznaczymy pole odcinka paraboli y = x²
o cięciwie o końcach A(a, a²), B(b, b²) .

Pomysł polega na wypełnianiu obszaru odcinka paraboli nieskończoną kolekcją specjalnych trójkątów. Owa kolekcja jest tworzona etapami. W pierwszym wybieramy jeden trójkąt.

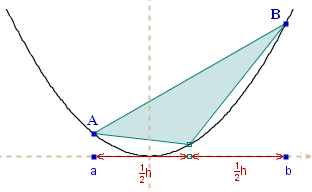
Kolejne etapy: 1,   2,   3,   4,   . . .

W każdym następnym etapie wybieramy dwa razy więcej trójkątów niż w poprzednim.
Pole odcinka paraboli jest sumą pól tych wszystkich (nieskończenie wielu) specjalnych trójkątów.

Co to są za specjalne trójkąty? Nazwijmy je A-trójkątami.
Wierzchołki A-trójkąta leżą na paraboli i pierwsza współrzędna 'środkowego' leży dokładnie w środku pomiędzy pierwszymi współrzędnymi 'skrajnych' wierzchołków.

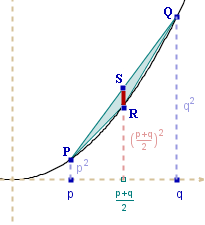Wyznaczmy wzór na pole takich specjalnych A-trójkątów:
 
Trójkąt PQR podzielmy odcinkiem RS prostopadłym do osi OX na dwa trójkąty o wspólnej podstawie RS . Obliczmy:
  |RS| = (p²+q²)/2 - ((p+q)/2)² =
        = p²/2 + q²/2 - p²/4 - q²/4 - 2pq/4 =
        = p²/4 + q²/4 - 2pq/4 = 1/4 ^. (q-p)² .
Stąd
(*)    pole trójkąta PQR = 2 ^. 1/2 ^. |RS| ^. |q-p|/2 = |q-p|³/8,

czyli: pole A-trójkąta jest równe 1/8 sześcianu odległości pierwszych współrzędnych jego 'skrajnych' wierzchołków.

(**)    Suma pól A-trójkątów z danego etapu jest 1/4 sumy pól trójkątów z poprzedniego etapu.

Faktycznie; z (*) wynika, że A-trójkąt z danego etapu ma pole równe 1/2³ części pola A-trójkąta z etapu poprzedniego.

Ćwiczenie 1.   Oblicz pole odcinka paraboli  y = x²  o cięciwie AB, gdzie:
  a)  A(0,0) i B(2,4)      b)  A(1,1) i B(3,9)      c)  A(,²) i B(4,16)      d)  A(,2) i B(,5)

Co wystarczy wiedzieć, by poniższe ćwiczenie było bardzo łatwe?

Ćwiczenie 2.   Oblicz pole odcinka paraboli  y = (x - 3)² - 2  o cięciwie AB, gdzie:
  a)  A(0,0) i B(2,4)      b)  A(1,1) i B(3,9)      c)  A(,²) i B(4,16)      d)  A(,2) i B(,5)

Co wystarczy zmienić w wyprowadzeniu ogólnego wzoru, by poniższe ćwiczenia były bardzo łatwe?

Ćwiczenie 3.   Oblicz pole odcinka paraboli  y = (3x-2)² - 1  o cięciwie AB, gdzie:
  a)  A(0,0) i B(2,4)      b)  A(1,1) i B(3,9)      c)  A(,²) i B(4,16)      d)  A(,2) i B(,5)

Ćwiczenie 4.   Oblicz pole odcinka paraboli  y = (2x-3)(3x-4)  o cięciwie AB, gdzie:
  a)  A(0,0) i B(2,4)      b)  A(1,1) i B(3,9)      c)  A(,²) i B(4,16)      d)  A(,2) i B(,5)

Problem 1.   Czy można nieznacznie zmodyfikować powyższe rozumowanie tak, by otrzymać wzór na pole odcinka paraboli, przy następującej modyfikacji pojęcia A-trójkąta:
Wierzchołki A'-trójkąta leżą na paraboli i pierwsza współrzędna 'środkowego' dzieli w skali 2:3 odcinek pomiędzy pierwszymi współrzędnymi 'skrajnych' wierzchołków.

Uwaga 1.   Już Archimedes potrafił obliczyć pole odcinka paraboli. Powyższe rozumowanie jest częsciowo wzorowane na jego pomyśle. Archimedes nie rachował, jego rozumowanie było geometryczne. (Na przykład umiał pokazać, że A-trójkąt ma największe pole wśród trójkątów zawartych w odcinku paraboli.) Ponadto jego rozumowanie było o wiele bardziej precyzyjne.

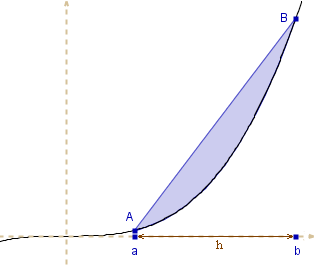Wykres funkcji y = x³, dla x 0, jest linią podobną do (połowy) paraboli.

Na rysunku obok widać obszar ograniczony linią y = x³ i cięciwą tej linii o końcach
A(a, a³), B(b, b³), 0<a<b.

Rozumowanie niewiele różni się od tego dla paraboli. Poza rachunkami zmienić trzeba dowód (**). Sprawdź.

Pomysł polega na wypełnianiu tego obszaru nieskończoną kolekcją specjalnych trójkątów. Owa kolekcja jest tworzona etapami. W pierwszym wybieramy jeden trójkąt.

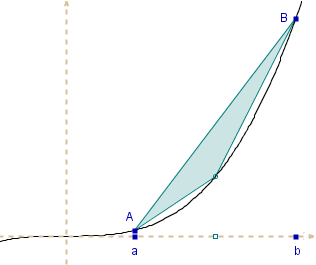
Kolejne etapy: 1,   2,   3,   4,   . . .

W każdym następnym etapie wybieramy dwa razy więcej trójkątów niż w poprzednim.
Pole obszaru jest sumą pól tych wszystkich (nieskończenie wielu) specjalnych trójkątów.

Co to są za specjalne trójkąty? Nazwijmy je A-trójkątami.
Wierzchołki A-trójkąta leżą na linii y = x³, x0, i pierwsza współrzędna 'środkowego' leży dokładnie w środku pomiędzy pierwszymi współrzędnymi 'skrajnych' wierzchołków.

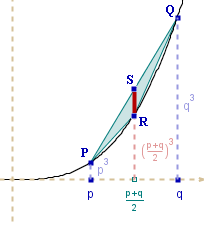Wyznaczmy wzór na pole takich specjalnych A-trójkątów:
 
Trójkąt PQR podzielmy odcinkiem RS prostopadłym do osi OX na dwa trójkąty o wspólnej podstawie RS . Sprawdź, że:
  |RS| = (p³+q³)/2 - ((p+q)/2)³ =
        = p³/2 + q³/2 - p³/8 - 3p²q/8 - 3pq²/8 - q³/8 =
        = 3/8 ^. (p³ + q³ - p²q - pq²) = 3/8 ^. (q-p)^{2 .} (p+q).
 
Stąd    pole trójkąta PQR = 2 ^. 1/2 ^. |RS| ^. |q-p|/2,  czyli
(*)    pole trójkąta PQR = 3/8 ^. |q-p|^{3 .} (p+q)/2,
czyli: 
pole A-trójkąta = iloczynowi 3/8 sześcianu odległości pierwszych współrzędnych jego 'skrajnych' wierzchołków
i pierwszej współrzędnej 'środkowego' wierzchołka.

(**)    Suma pól A-trójkątów z danego etapu jest 1/4 sumy pól trójkątów z poprzedniego etapu.

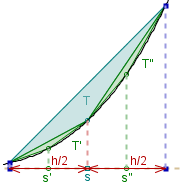
Faktycznie:
Niech A-trójkąty T ', T '' z danego etapu 'leżą pod' A-trójkątem T z poprzedniego etapu, niech s', s'' i s oznaczają pierwsze współrzędne ich 'środkowych' wierzchołków oraz h - odległość pierwszych współrzędnych 'skrajnych' wierzchołków trójkąta T.
Stosując (*) mamy wtedy:
pole T ' + pole T '' = 3/8 (h/2)^{3 .} s' + 3/8 (h/2)^{3 .} s'' =
= 1/4 ^. 3/8 h^{3 .} (s'+s'')/2 = 1/4 ^. 3/8 h^{3 .} s = 1/4 ^. pole T.

Uwaga 2. (tylko dla dorosłych)   Rachunek całkowy Newtona-Leibniza upraszcza radykalnie oba powyższe rozumowania.