Niech k oznacza ustaloną prostą i O punkt poza tą prostą.
Miejsca jednakowo odległe od O i od k tworzą linię zwaną parabolą. Oznaczmy ją Par(O,k).

Zadanie 0. 
Jak wyznaczać punkty paraboli Par(O,k)?

Rozwiązanie.  Dla zadanego punktu P' na prostej k, punkt P przecięcia symetralnej odcinka OP' i prostej prostopadłej do k przechodzącej przez P' jest punktem paraboli Par(O,k).
(Zobaczy kroki konstrukcji; kliknij .)

Uwaga.  
Dla (dowolnego) punktu Z przez Z' oznaczmy taki punkt na k, że ZZ' jest odległością Z od k, czyli prosta Z'Z jest prostopadła do k.
Dla punktu P paraboli Par(O,k) przez s_P oznaczamy symetralną odcinka OP'.

Zadanie 1. 
Niech punkt P leży na paraboli Par(O,k).
Niech punkt X 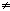P leży na prostej s_P Uzasadnij, że

Rozwiązanie.  
   OX = XP'   (bo X leży na symetralnej),
   XP' > XX'   (bo przeciwprostokątna jest dłuższa
                        od przyprostokątnej).
skąd
   OX > XX'     (dokończ rysunek).

Zadanie 2. 
Niech punkt P leży na paraboli Par(O,k). i niech punkt Y leży po przeciwnej stronie prostej s_P niż punkt O.
Uzasadnij, że

Rozwiązanie.  
Niech X oznacza punkt przecięcia s_P i OY.
   OY  =  P'X + XY  >  P'Y    Y'Y ,
gdzie:
   ' = ' - wynika z własności symetralnej,
   ' > ' - wynika z nierówności trójkąta,
   ' ' - wynika z faktu, że Y'Y jest najkrótszym odcinkiem łączącym Y z k.

Wniosek A.   Proste s_P są podpierającymi, tzn. parabola leży po jednej stronie prostej s_P.
(To 'niemal' to samo co stwierdzenie: s_P są stycznymi do paraboli.)

Zadanie 3. 
Niech punkt Z leży 'pod' parabolą. Skonstruuj taki punkt P paraboli Par(O,k), że

Wskazówka.  
Najpierw znajdź punkt P'.

Rozwiązanie.  
Okrąg o środku Z, przechodzący przez O, wyznacza w przecięciu z prostą k punkt P'. Dalej - jak w Zadaniu 0.

Uwaga.  
Są dwa takie punkty. Narysuj oba.

Zadanie 4. 
Niech punkt P leży na paraboli Par(O,k) i punkt P'' leży na półprostej P'P poza odcinkiem P'P.
Niech n_P będzie prostą prostopadłą do s_P przechodzącą przez punkt P.
Uzasadnij, że

n_P jest dwusieczną kąta OPP'',
czyli    | 0PN |  =  | NPP'' | .

Rozwiązanie.  
Odbijając kąt 0PN w prostej s_P, dostaniemy kąt wierzchołkowy z kątem NPP''.

Wniosek B.  Promienie z żarówki umieszczonej w punkcie O, po odbiciu od paraboli utworzą równoległą wiązkę światła.

Wniosek B'.  Lusterko w kształcie paraboloidy obrotowej (= powierzchni powstałej z obrotu paraboli względem jej osi symetrii OO'), ustawione osią symetrii w kierunku słońca, skupi promienie słoneczne w punkcie O (ognisko).

Zadanie 5. 
Niech punkt P leży na paraboli Par(O,k).
Niech punkty K,L leżą na prostej s_P tak, że P jest środkiem odcinka KL.
Uzasadnij, że

Rozwiązanie.  
Trójkąt KLP', będący odbiciem trójkąta KL0, jest połową trapezu KK'L'LL. Można to sprawdzić rachunkiem albo inaczej:
'rozetnij' trapez wzdłuż PP' i obróć jedną z części (np. KK'P'P) o 180^o względem P; wtedy z trapezu powstaje 'chudy' prostokąt, będący w połowie czerwony (kliknij ).

Wniosek C. 
Niech P,Q leżą na paraboli Par(O,k).
Parabola dzieli wielokąt OPP'Q'Q
na dwa obszary, których stosunek pól jest równy 2 : 1.

Dowód (szkic). 
Stosujemy n razy tezę Zadania 5 dla wielokątów przybliżających owe obszary.
(Na rysunku zwiększ n przesuwając czerwoną kropkę.)
Możliwość budowania takich przylegających trapezów (i trójkątów) wynika z tezy Zadania 3.

Zadanie 6. 
Niech P,Q leżą na paraboli Par(O,k).
Niech punkt K będzie punktem przecięcia prostej s_P i symetralnej odcinka P'Q'.
Uzasadnij, że

Rozwiązanie.  
   OK = KP'   (bo K leży na symetralnej s_P),
   KP' = KQ'   (bo K leży na symetralnej odcinka P'Q'),
stąd
   OK = KQ' ,
czyli K leży na s_Q, symetralnej odcinka OQ'.

Zadanie 7. 
Niech P,Q,R leżą na paraboli Par(O,k) tak, że R' leży na symetralnej odcinka P'Q'.
Niech punkt K będzie punktem przecięcia prostej s_P i symetralnej odcinka P'Q'.
Uzasadnij, że

Rozwiązanie.  
Wystarczy dwukrotnie zastosować Zadanie 6.
Raz - dla punktów P, R i prostej s_P,
drugi raz - dla punktów Q, R i prostej s_Q.

Zadanie 8. 
Niech P,Q,R leżą na paraboli Par(O,k) tak, że R' leży na symetralnej odcinka P'Q'.
Uzasadnij, że

Rozwiązanie.  
Proste s_P i s_Q przecinają się w punkcie K, leżącym na symetralnej odcinka P'Q' (z Zadania 6.), więc na prostej RR'. Z Zadania 7. wynika, że s_R połowi boki PK, KQ trójkąta PQK. Zatem s_R jest równoległa do PQ (z tw. Talesa).

Zadanie 9. 
Niech P,Q leżą na paraboli Par(O,k)
i niech K będzie punktem przecięcia prostych s_P i s_Q. Niech L oznacza środek odcinka PQ.
Uzasadnij, że

Rozwiązanie.  
Z Zadania 8. wynika, że jeśli na symetralnej odcinka P'Q' leży jakiś punkt paraboli, to leży na odcinku połowiącym boki PK, KQ trójkąta PQK, skąd wynika, że pokrywa się on ze środkiem odcinka LK.
Istnienie punktu paraboli na prostej KK' wynika z Zadania 0. (podstawiając K' w miejsce P').

Zadanie 10. 
Niech P,Q leżą na paraboli Par(O,k)
i niech K będzie punktem przecięcia prostych s_P i s_Q. Niech L oznacza środek odcinka PQ i niech M i N oznaczają środki odcinków PK i PL
Parabola dzieli odcinek MN; w jakim stosunku?

Rozwiązanie.  
Z Zadania 10. wynika, że R - środek odcinka KL jest punktem paraboli.
Niech Z oznacza środek odcinka PR. Z jest oczywiście również środkiem odcinka MN (z tw. Talesa).
Stosując Zadanie 10. do punktów P,R otrzymamy:
środek odcinka ZM jest punktem paraboli.
Zatem parabola dzieli MN w stosunku 1 : 3.

Uwaga. 
Na rysunku pokazano jak, mając punkty P, Q paraboli i proste s_P, s_Q, wyznaczać dalsze punkty paraboli (te czerwone). Czerwone punkty są środkami odcinków o czarnych końcach o numerach o jeden mniejszych. (Na rysunku punkty, które wydają się środkami pewnych odcinków są faktycznie środkami.)
Liczby pokazują kolejność konstrukcji.
 
Czarne trójkąty coraz lepiej wypełniają obszar nad parabolą zawarty w trójkącie PQK. Obliczając sumę ich pól Archimedes pokazał, że obszar nad parabolą w trójkącie PQK ma pole równe 2/3 pola tego trójkąta.
Poniżej pokażemy to trochę inaczej.

Zadanie 11*. 
Niech P,Q leżą na paraboli Par(O,k)
i niech K będzie punktem przecięcia prostych s_P i s_Q. Niech P'', Q'' leżą na odcinkach PP' i QQ' tak, że P''Q'' || PQ i K leży na P''Q''.
Uzasadnij, że:
a)  pole PKO + pole QKO = pole PKP' + pole QKQ',
b)  pole P'KP'' + pole Q'KQ'' = pole PQO,
c)  pole P'P''Q''Q' = 2 ^. pole PQO,
d)  parabola dzieli obszar P''PQQ'' w stosunku 2 : 1,
e)  obszar nad parabolą w trójkącie PQK ma pole równe 2/3 pola tego trójkąta.

Rozwiązanie.  
Może jednak spróbuj sam!
To nie jest takie trudne, gdy użyjesz tezy Wniosku C.

Zadanie 12*. 
Mając tylko punkty P,Q paraboli Par(O,k) i proste s_P i s_Q skonstruuj prostą k i punkt O.

Rozwiązanie.   (szkic)
Bazując na Zadaniu 9., znajdujemy kierunek prostych prostopadłych do k.
Dalej, dzięki Zadaniu 4., wyznaczamy O.
Na koniec łatwo wyznaczamy P', zatem i prostą k.