W wielu podręcznikach rzut ukośny jest omawiany z użyciem trygonometrii i pochodnych. Okazuje się, że gdy 'zaufamy wektorom', to nie trzeba aż takiej wiedzy z matematyki, wystarczy właściwie twierdzenie Pitagorasa (+ fizyka!).

Problem. 
Rzut ciała: o masie m = 0,1kg, z szybkością v₀ = 30m/s, pod kątem , z wysokości h = 35m.
Dla jakiego zasięg jest największy?

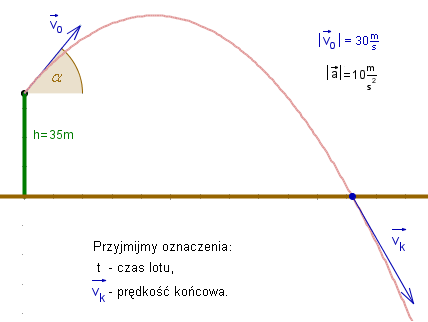
Zacznijmy od tego, że nie wieje wiatr i opory powietrza pomijamy. Zatem na ciało działa jedynie STAŁA siła przyciągania skierowana pionowo w dół. Siła ta (jak mówi Newton) zmienia prędkość ciała. Zmiana prędkości w jednostce czasu to jest przyśpieszenie, precyzyjniej: różnica prędkości podzielona przez czas, to jest średnie przyśpieszenie (ważne, że tu chodzi o wektory!):

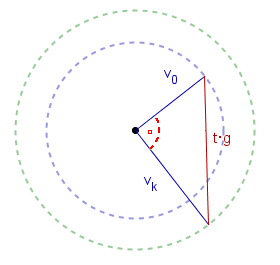
Ponieważ siła jest STAŁA, to przyśpieszenie jest STAŁE, skierowane w dół, równe g=10m/s². Równość ta jest pokazana na rysunku (zaczepiamy wektory prędkości w jednym punkcie).

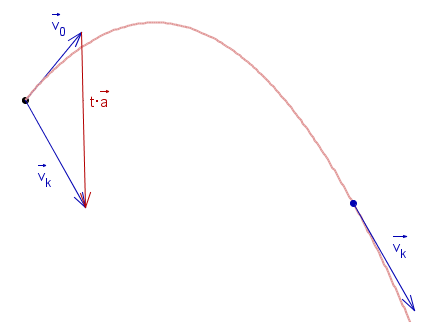
Uwaga. Fizycy ten 'trójkąt' przeczytają (mnożąc boki przez m): popęd jest równy zmianie pędu.

Teraz najważniejsze: szybkość przy lądowaniu (wielkość ) jest stała, tj. nie zależy od kąta . Mianowicie energia na początku i końcu jest taka sama: E₀ = E_k, czyli

skąd (po łatwym rachunku) otrzymamy

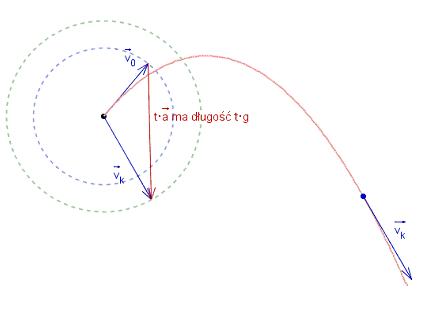
Zaznaczmy na rysunku okręgi o promieniach równych i , to na nich leżą końce pionowego odcinka, niezależnie od kąta .

 

 
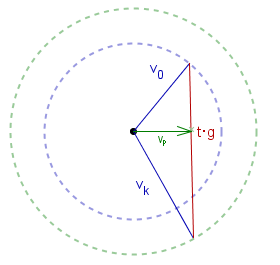
Dorysujmy 'poziomą' wysokość tego trójkąta (prostopadłą do pionowego boku). Ma ona długość v_p składowej poziomej wektora .
Pole tego trójkąta jest równe  

^. v_p ^. t g = (v_p^.t ) ^. (g) ,   czyli jest równe (zasięg) ^. (g)   .

 

 
Zatem

zasięg jest największy, gdy pole jest największe,
pole jest największe, gdy boki są prostopadłe.

 

 
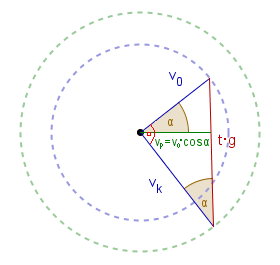
Wtedy z takiego trójkąta prostokątnego można niemal wszystko odczytać.

Mianowicie w locie o maksymalnym zasięgu:

-   kąt, pod którym ciało będzie wbijać się w ziemię jest równy 90^o - ,

-   zasięg jest równy polu trójkąta podzielonemu przez g, czyli

     podstawiając liczby:    

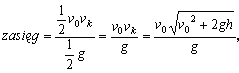
-   lot będzie trwał (z tw. Pitagorasa wyznaczamy przeciwprostokątną skąd znajdujemy czas t )

     podstawiając liczby:    

-   zasięg maksymalny otrzymamy przy rzucie pod kątem , którego tangens jest równy

     podstawiając liczby:         skąd 37^o.

 

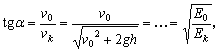
UWAGA. Tak rozwiązywane zadania można znaleźć w świetnej książce: 'Matematyka w szkole średniej', tomy 1, 2, 3, WSiP, Warszawa 1988r., (tłumaczenie podręcznika angielskiego wydanego przez Cambridge University Press).