10. Przestrzenie euklidesowe

Student poznał już standardowy iloczyn skalarny wektorów w przestrzeni ${\mathbb{R}}^n$. Używając tego pojęcia możemy zdefiniować w przestrzeni ${\mathbb{R}}^n$ pojęcia długości wektora i odległości między wektorami. Możemy również określić kąt między dwoma wektorami. Dzięki temu łatwiej możemy sobie wyobrażać przestrzeń ${\mathbb{R}}^n$. Dla tych zastosowań iloczynu skalarnego w przestrzeni ${\mathbb{R}}^n$ istotne są pewne własnosci, które ten iloczyn posiada. Z uwagi na korzyści, jakie daje iloczyn skalarny w przestrzeni ${\mathbb{R}}^n$ warto wprowadzić pojęcie abstrakcyjnego iloczynu skalarnego w dowolnej przestrzeni liniowej nad ciałem liczb rzeczywistych. Uczynimy to zaraz w poniższej definicji. Należy jednak zastrzec się w tym miejscu, że pojęcia iloczynu skalarnego nie definiujemy w przestrzeni liniowej nad dowolnym ciałem $K$. W praktyce najważniejszy jest iloczyn skalarny w rzeczywistych przestrzeniach liniowych. Można również zdefiniować pojęcie iloczynu skalarnego w zespolonych przestrzeniach liniowych. Teraz jednak skoncentrujemy sie na przestrzeniach liniowych nad ${\mathbb{R}}$.

Załóżmy więc, że $V$ jest przestrzenią liniową nad ${\mathbb{R}}$.

Definicja 10.1   Iloczynem skalarnym w przestrzeni $V$ nazywamy dowolną funkcję $\langle\cdot,\cdot\rangle:V\times V\rightarrow {\mathbb{R}}$ taką, że dla wszystkich $v,v',w\in V$ i $t\in {\mathbb{R}}$ mamy:
1. (symetryczność) $\langle v,w\rangle=\langle w,v\rangle$
2. (liniowość na 1. współrzędnej)
$\langle v+v',w\rangle=\langle v,w\rangle+\langle v',w\rangle$ i $\langle tv,w\rangle=t\langle v,w\rangle$
3. (dodatnia określoność) $\langle v,v\rangle>0$ dla $v\neq O$.

Przestrzeń liniową $(V,\langle\cdot,\cdot\rangle)$ z określonym w niej iloczynem skalarnym nazywamy przestrzenią euklidesową.

Zwróćmy uwagę, że z uwagi na symetryczność, liniowość iloczynu skalarnego na 1. współrzędnej implikuje liniowość na 2. współrzędnej:

2'.

$\langle v,w+w'\rangle=\langle v,w\rangle+\langle v,w'\rangle\mbox{ i } \langle v,tw\rangle=t\langle v,w\rangle.$

Zazwyczaj w przestrzeni $V$ istnieje wiele funkcji $\langle\cdot,\cdot\rangle$ spełniających warunki definicji iloczynu skalarnego. Poniżej podajemy kilka przykładów iloczynu skalarnego w różnych przestrzeniach.

Przykłady.

1. Standardowy iloczyn skalarny w ${\mathbb{R}}^n$. Dla wektorów

$$X=\left[\begin{array}{c}x_1 \vdots x_n\end{array}\right],... ...array}{c}y_1 \vdots y_n\end{array}\right]\in {\mathbb{R}}^n$$

definiujemy $\langle X,Y\rangle=X\cdot Y=\sum_ix_iy_i$.

2. W przestrzeni wielomianów ${\mathbb{R}}[X]$ możemy zdefiniować iloczyn skalarny wzorem

$$\langle f,g\rangle=\int_0^1 f(x)g(x)dx.$$

3. Rozważmy macierz $A=[a_{ij}]_{n\times n}$. Określamy funkcję 2-argumentową $\Phi_A:{\mathbb{R}}^n\times {\mathbb{R}}^n\rightarrow {\mathbb{R}}^n$ wzorem

$$\Phi_A(X,Y)=X^*AY.$$

We wzorze tym wektory $X,Y$ traktujemy jak macierze wymiaru $n\times 1$, zatem $X^*$ to macierz transponowana względem $X$, wymiaru $1\times n$, czyli po prostu wiersz złożony z kolejnych współrzędnych wektora $X$. ściśle rzecz biorąc, $\Phi_A(X,Y)$ to macierz wymiaru $1\times 1$. Macierze takie utożsamiamy z liczbami rzeczywistymi. Po wykonaniu działań występujących we wzorze na $\Phi_A$ otrzymujemy wzór na $\Phi_A$ zależny od współrzędnych wektorów $X,Y$.

$$\Phi_A(X,Y)=\sum_{1\leq i,j\leq n}a_{ij}x_iy_j$$

Funkcja $\Phi_A$ spełnia warunki (2) i (2') definicji iloczynu skalarnego (tzn. jest liniowa względem obu współrzędnych). Dla przykładu sprawdzimy addytywność na 1. współrzędnej.

$$\Phi_A(X+X',Y)=(X+X')^*AY=(X^*+(X')^*)AY=$$

$$X^*AY+(X')^*AY=\Phi_A(X,Y)+\Phi_A(X',Y)$$

Gdy macierz $A$ jest symetryczna, funkcja $\Phi_A$ spełnia również warunek 10.1(1). Jeśli dodatkowo funkcja $\Phi_A$ spełnia warunek 10.1(4)(dodatnia określoność), to jest ona iloczynem skalarnym w ${\mathbb{R}}^n$.

Problem. Dla jakich macierzy symetrycznych $A$ funkcja $\Phi_A$ jest dodatnio określona ?

Problemem tym zajmiemy się później.

4. Niech $l^2$ będzie zbiorem ciągów $(a_n)_{n\in N}$ liczb rzeczywistych takich, że $\sum_{n=0}^{\infty}a_n^2<\infty$. łatwo sprawdzić, że zbiór ten jest podprzestrzenią przestrzeni liniowej $\prod_{n\in N}{\mathbb{R}}$ (pozostawiamy to jako ćwiczenie).

W przestrzeni $l^2$ określamy iloczyn skalarny wzorem

$$\langle(a_n),(b_n)\rangle=\sum_na_nb_n.$$

Sprawdzenie, że w istocie wzór ten definiuje iloczyn skalarny pozostawiamy jako ćwiczenie.

5. Niech $C(I)$ oznacza przestrzeń liniową ciągłych funkcji $f:I\rightarrow {\mathbb{R}}$ ($I=[0,1]$). Działania w tej przestrzeni liniowej określamy podobnie, jak w przestrzeni $C({\mathbb{R}})$ funkcji ciągłych na ${\mathbb{R}}$.

W przestrzeni $C(I)$ definiujemy iloczyn skalarny wzorem

$$\langle f,g\rangle=\int_0^1 f(x)g(x)dx.$$

Przestrzeń euklidesową $({\mathbb{R}}^n,\langle\cdot,\cdot\rangle)$ ze standardowym iloczynem skalarnym oznaczamy symbolem $E^n$.

Od tej pory w tym rozdziale zakładamy, że $V$ jest przestrzenią euklidesową z iloczynem skalarnym $\langle\cdot,\cdot\rangle$. Podobnie jak w przypadku przestrzeni ${\mathbb{R}}^n$ ze standardowym iloczynem skalarnym przyjmujemy następującą definicję.

Definicja 10.2   Długość (normę) wektora $v\in V$ definiujemy jako liczbę $\Vert v\Vert=\sqrt{\langle v,v\rangle}$.

Następująca uwaga zawiera podstawowe własności iloczynu skalarnego.

Uwaga 10.3   0) $\Vert tv\Vert=\vert t\vert\cdot\Vert v\Vert$
1) (nierówność Cauchy'ego-Schwarza) $\vert\langle v,w\rangle\vert\leq\Vert v\Vert\cdot\Vert w\Vert$
2) (nierówność Minkowskiego) $\Vert v+w\Vert\leq\Vert v\Vert+\Vert w\vert\Vert$
3) $\Vert v\Vert-\Vert w\Vert\leq\Vert v-w\Vert$

Dowód. 0). $\Vert tv\Vert=\sqrt{\langle tv,tv\rangle}=\sqrt{t^2\langle v,v\rangle}=\vert t\vert\sqrt{\langle v,v\rangle}=\vert t\vert\cdot\Vert v\Vert$.

1) łatwo sprawdzić (1), gdy $v,w$ są liniowo zależne (wówczas w (1) mamy nawet $=$). Załóżmy więc, że $v,w$ są liniowo niezależne. Rozważmy funkcję $f:{\mathbb{R}}\rightarrow {\mathbb{R}}$ zdefiniowaną wzorem

$$f(t)=\Vert v-tw\Vert^2.$$

Zauważmy, że skoro $v,w$ są liniowo niezależne, funkcja $f$ przyjmuje zawsze wartości dodatnie. Korzystając z liniowości iloczynu skalarnego na obu współrzędnych dostajemy

$$f(t)=\langle v-tw,v-tw\rangle=\langle v-tw,v\rangle+\langle v-tw,-tw\rangle=$$

$$\langle v,v\rangle+\langle -tw,v\rangle+\langle v, -tw\rangle+\langle -tw,-tw\rangle=$$

$$\Vert v\Vert^2-2t\langle v,w\rangle +t^2\Vert w\Vert^2>0$$

dla wszystkich $t\in {\mathbb{R}}$. Równanie $f(t)=0$ jest więc równaniem kwadratowym o niewiadomej $t$, bez rozwiązań rzeczywistych. Dlatego wyróżnik tego równania jest ujemny.

$$\Delta= 4\langle v,w\rangle^2-4\Vert v\Vert^2\cdot\Vert w\Vert^2<0$$

Stąd natychmiast dostajemy nierówność Schwarza.

2) Korzystając z (1) dostajemy

$$\Vert v+w\Vert^2=\langle v+w,v+w\rangle=\Vert v\Vert^2+\Vert w\Vert^2+2\langle v,w\rangle\leq$$

$$\Vert v\Vert^2+\Vert w\Vert^2+2\Vert v\Vert\cdot\Vert w\Vert=(\Vert v\Vert+\Vert w\Vert)^2.$$

3) wynika z (2).

W przestrzeni euklidesowej definiujemy odległość $d(v,w)$ między wektorami $v,w\in V$ wzorem

$$d(v,w)=\Vert v-w\Vert.$$

Z nierówności Minkowskiego otrzymujemy łatwo nierówność trójkąta :

$$d(v,w)\leq d(v,u)+d(u,w)$$

dla wszystkich $u,v,w\in V$.

Na mocy nierówności Schwarza, dla wszystkich niezerowych wektorów $v,w\in V$ mamy

$$-1\leq\frac{\langle v,w\rangle}{\Vert v\Vert\cdot\Vert w\Vert}\leq 1.$$

Dlatego możemy zdefiniować kąt (nieskierowany) między wektorami $v,w$ jako jedyną liczbę $\alpha\in[0,\pi]$ taką, że

$$\cos(\alpha)=\frac{\langle v,w\rangle}{\Vert v\Vert\cdot\Vert w\Vert}.$$

W następnym rozdziale poznamy głębsze uzasadnienie definicji odległości i kąta między wektorami w przestrzeni euklidesowej.

Jak wspomnieliśmy na wstępie tego rozdziału, iloczyn skalarny można zdefiniować również w zespolonych przestrzeniach liniowych. Musimy wówczas jednak nieco zmodyfikować definicję 10.1.

Standardowy iloczyn skalarny $\langle\cdot,\cdot\rangle:{\mathbb{C}}^n\times {\mathbb{C}}^n\rightarrow {\mathbb{C}}$ w zespolonej przestrzeni liniowej ${\mathbb{C}}^n$ definiujemy wzorem

$$\langle Z,Z'\rangle=\sum_{i=1}^n z_i\overline{z_i}',\mbox{ gd... ...y}{c}z'_1 \vdots\\ z'_n\end{array}\right]\in {\mathbb{C}}^n.$$

Zwróćmy uwagę, że $\langle Z,Z\rangle$ jest liczbą rzeczywistą $\geq 0$. Długość wektora $Z$ definiujemy jako liczbę $\Vert Z\Vert=\sqrt{\langle Z,Z\rangle}$, podobnie jak w przestrzeni euklidesowej. Przestrzeń $C^n$ możemy traktować jako rzeczywistą przestrzeń liniową (ograniczając mnożenie przez skalary do skalarów rzeczywistych), izomorficzną z ${\mathbb{R}}^{2n}$: wektor $Z\in {\mathbb{C}}^n$ odpowiada tu wektorowi $X_Z\in {\mathbb{R}}^{2n}$ o kolejnych współrzędnych $x_1,y_1,x_2,y_2,\dots,x_n,y_n$, gdzie $z_t=x_t+iy_t$. Okazuje się, że długość wektora $X_Z$ w przestrzeni ${\mathbb{R}}^{2n}$ (ze standardowym iloczynem skalarnym) równa się długości wektora $Z$:

$$\Vert X_Z\Vert=\sqrt{(x_1^2+y_1^2)+\cdots+(x_n^2+y_n^2)}=$$

$$\sqrt{z_1\cdot\overline{z_1}+\cdots+z_n\cdot\overline{z_n}}=\sqrt{\langle Z,Z\rangle}=\Vert Z\Vert.$$

Definicja 10.4   W dowolnej zespolonej przestrzeni liniowej $W$ iloczynem skalarnym nazywamy dowolną funkcję $\langle\cdot,\cdot\rangle:W\times W\rightarrow {\mathbb{C}}$ spełniającą następujące warunki dla wszystkich $v,v',w\in W$ i $t\in {\mathbb{C}}$:
1. $\langle v,w\rangle=\overline{\langle w,v\rangle}$
2. (liniowość na 1. współrzędnej)
$\langle v+v',w\rangle=\langle v,w\rangle+\langle v',w\rangle,\ \langle tv,w\rangle=t\langle v,w\rangle$
3. $\langle v,v\rangle\geq 0$

Warunek 10.4(1) implikuje, że $\langle v,v\rangle$ jest liczbą rzeczywistą, dlatego warunek 10.4(3) ma sens. Podobnie jak w przypadku rzeczywistego iloczynu skalarnego, warunki 10.4(1) i 10.4(2) implikują warunek (2') poniżej

2'.

(antyliniowość na 2. współrzędnej)
$\langle v,w+w'\rangle=\langle v,w\rangle+\langle v,w'\rangle,\ \langle v,tw\rangle=\overline{t}\langle v,w\rangle$.

łatwo sprawdzić, że standardowy iloczyn skalarny w ${\mathbb{C}}^n$ spełnia warunki definicji 10.4. Zespoloną przestrzeń liniową $(W,\langle\cdot,\cdot\rangle)$ z iloczynem skalarnym $\langle\cdot,\cdot\rangle$ nazywamy przestrzenią unitarną.

Można udowodnić, że uwaga 10.3 jest słuszna również dla zespolonego iloczynu skalarnego (ćwiczenie). Większość rozumowań dotyczących rzeczywistego iloczynu skalarnego przenosi się łatwo na iloczyn zespolony. (Wyjątkiem jest tu pojęcie kąta między wektorami, którego nie definiujemy w przestrzeni unitarnej).

W dalszym ciągu będziemy zajmować się przestrzenią euklidesową $V$. Podobnie jak w przypadku przestrzeni $E^n$ przyjmujemy następującą definicję.

Definicja 10.5   1) Wektory $v,w\in V$ są ortogonalne (symbolicznie:
$v\perp w$) $\iff\langle v,w\rangle=0$.
2) Dla zbiorów $A,B$ piszemy $A\perp B$ gdy $v\perp w$ dla wszystkich $v\in A$ i $w\in B$. Gdy $A=\{v\}$, piszemy $v\perp B$ zamiast $A\perp B$.
3) Dla $X\subset V$ definiujemy zbiór $X^{\perp}=\{v\in V:v\perp X\}$. Zbiór $X^{\perp}$ nazywamy dopełnieniem ortogonalnym zbioru $X$ w przestrzeni $V$.

Uwaga 10.6   1) Dla niezerowych wektorów $v,w\in V, v\perp w\iff$ kąt między wektorami $v,w$ równa się $\pi/2$.
2) $X^{\perp}$ jest podprzestrzenią $V$.

Dowód. 1) jest oczywiste.

2) Sprawdzamy, że zbiór $X^{\perp}$ jest zamknięty ze względu na działania przestrzeni liniowej. Np. sprawdzimy zamkniętość względem dodawania. Załóżmy, że $v,w\in X^{\perp}$. Wówczas również $v+w\in X^{\perp}$, bo dla dowolnego $x\in X$ mamy

$$\langle v+w,x\rangle=\langle v,x\rangle+\langle w,x\rangle=0+0=0.$$

Definicja 10.7   1) Mówimy że wektor $v\in V$ jest unormowany (inaczej : jednostkowy), gdy ma długość $1$.
2) Bazę przestrzeni $V$ złożoną z wektorów parami ortogonalnych nazywamy bazą ortogonalną.
3) Bazę ortogonalną przestrzeni $V$ złożoną z wektorów unormowanych nazywamy bazą ortonormalną.

Przykładem bazy ortonormalnej w $E^n$ jest baza standardowa ${\cal E}$.

Załóżmy, że $v\in V$ jest niezerowy, niech $t=\Vert v\Vert^{-1}$. Wówczas wektor $tv$ jest już unormowany. Dlatego, mając bazę ortogonalną przestrzeni $V$ łatwo otrzymać bazę ortonormalną, odpowiednio wydłużając lub skracając wektory bazowe.

Zastosowania.

1. Załóżmy, że ${\cal B}=\{b_1,\dots,b_n\}$ jest bazą ortonormalną przestrzeni $V$. Następna uwaga pokazuje, jak łatwo znaleźć współrzędne $[v]_{{\cal B}}$ wektora $v$ w bazie ${\cal B}$.

Uwaga 10.8   Dla wektora $v\in V, v=\sum\langle v,b_i\rangle b_i$, tzn.

$$[v]_{{\cal B}}=\left[\begin{array}{c}\langle v,b_1\rangle \vdots\\ \langle v,b_n\rangle \end{array}\right].$$

Dowód. Wiemy, że $v=\sum t_ib_i$ dla pewnych $t_i\in R$. Skoro baza ${\cal B}$ jest ortonormalna, to

$$\langle b_i,b_j\rangle=\left\{\begin{array}{ll}0,&\mbox{gdy } i\neq j\\ 1,&\mbox{ gdy } i=j,\end{array}\right.$$

Dlatego $\langle v,b_i\rangle=\langle\sum_jt_jb_j,b_i\rangle=\sum_jt_j\langle b_j,b_i\rangle=t_i\langle b_i,b_i\rangle=t_i$.

Załóżmy teraz, że $F:V\rightarrow V$ jest liniowe. Wektory $[F(b_j)]_{{\cal B}}$ tworzą kolejne kolumny macierzy $m_{{\cal B}}(F)$. Współrzędne wektora $[F(b_j)]_{{\cal B}}$ są postaci $\langle b_i,F(b_j)\rangle$. Dlatego $m_{{\cal B}}(F)=[\langle b_i,F(b_j)\rangle]_{n\times n}$.

2. Załóżmy, że $W$ jest podprzestrzenią przestrzeni $V$ oraz ${\cal B}=\{b_1,\dots,b_k\}$ jest bazą ortonormalną przestrzeni $W$. Używając tej bazy możemy łatwo zdefiniować rzut prostopadły $P_W:V\rightarrow V$ przestrzeni $V$ na podprzestrzeń $W$ wzorem

$$P_W(v)=\sum_{i=1}^k\langle v,b_i\rangle b_i.$$

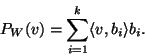
Następująca uwaga uzasadnia, że w istocie tak określone przekształcenie $P_W$ możemy uważać za rzut prostopadły na $W$.

Uwaga 10.9   1) $P_W:V\rightarrow V$ jest liniowe.
2) Dla $v\in W, P_W(v)=v$.
3) Dla $v\in V, P_W(v)$ jest jedynym wektorem podprzestrzeni $W$ takim, że $v-P_W(v)\perp W$.

Dowód. 1) Sprawdzimy np. addytywność $P_W$.

$$P_W(v_1+v_2)=\sum\langle v_1+v_2,b_i\rangle=\sum(\langle v_1,b_i\rangle+\langle v_2,b_i\rangle) b_i=$$

$$\sum\langle v_1,b_i\rangle b_i+\sum\langle v_2,b_i\rangle b_i=P_W(v_1)+P_W(v_2)$$

2) Na mocy uwagi 10.8 (zastosowanej do przestrzeni $W$ z bazą ortonormalną ${\cal B}$), $v=\sum\langle v,b_i\rangle b_i=P_W(v)$.

3) Po pierwsze sprawdzimy, że

$$(*) v-P_W(v)\perp W.$$

Istotnie, rozważmy dowolny wektor $w=\sum t_ib_i$ przestrzeni $W$. Mamy

$$\langle v,w\rangle=\langle v,\sum t_ib_i\rangle=\sum t_i\langle v,b_i\rangle.$$

Z drugiej strony

$$\langle P_W(v),w\rangle=\langle \sum\langle v,b_i\rangle b_i,... ...b_i\rangle\langle b_i,b_j\rangle=\sum_it_i\langle v,b_i\rangle,$$

gdyż

$$\langle b_i,b_j\rangle=\left\{\begin{array}{ll}0,&\mbox{gdy } i\neq j\\ 1,&\mbox{ gdy } i=j.\end{array}\right.$$

Dlatego $\langle v,w\rangle=\langle P_W(v),w\rangle$, więc

$$\langle v-P_W(v),w\rangle=\langle v,w\rangle-\langle P_W(v),w\rangle=0.$$

Pozostaje pokazać, że wektor $P_W(v)$ jest jedynym wektorem podprzestrzeni $W$ spełniającym $(*)$. W tym celu przypuśćmy, że $v'\in W$ i $v-v'\perp W$. Pokażemy, że wówczas $v'=P_W(v)$.

Skoro $v-v'\perp W$, to tym bardziej $v-v'\perp b_i$ dla $i=1,\dots,k$. Dlatego $0=\langle v-v',b_i\rangle=\langle v,b_i\rangle-\langle v',b_i\rangle$, czyli $\langle v,b_i\rangle=\langle v',b_i\rangle$.

Na mocy uwagi 10.8 (podobnie jak w (2)),

$$v'=\sum\langle v',b_i\rangle b_i=\sum\langle v,b_i\rangle b_i=P_W(v).$$

Przykład.

Niech $u=\frac{1}{\sqrt{3}}\left[\begin{array}{c}1\\ 1 1\end{array}\right], v=\frac... ...eft[\begin{array}{c}0\\ 1 -1\end{array}\right],w=u\times v\in {\mathbb{R}}^3$. Niech $\Pi=Lin(u,v)$ będzie płaszczyzną generowaną przez $u,v$. Wówczas ${\cal B}=\{u,v,w\}$ jest bazą ortonormalną przestrzeni ${\mathbb{R}}^3$, zaś ${\cal C}=\{u,v\}$ bazą ortonormalną podprzestrzeni $\Pi$.

Rzut prostopadły wektora $X\in {\mathbb{R}}^3$ na płaszczyznę $\Pi$ wyraża się wzorem

$$(*) P_{\Pi}(X)=\langle X,u\rangle u+\langle X,v\rangle v.$$

Ze wzoru tego łatwo odczytać macierz $m(P_{\Pi})$ przekształcenia $P_{\Pi}$ w bazie standardowej. Inny sposób znalezienia tej macierzy polega na obliczeniu zgodnie ze wzorem $(*)$ wektorów $P_{\Pi}(E_1),P_{\Pi}(E_2)$ i $P_{\Pi}(E_3)$, tworzących kolejne kolumny macierzy $m(P_{\Pi})$.

Ponadto zgodnie z uwagą 10.8 łatwo znaleźć współrzędne wektora $X\in {\mathbb{R}}^3$ w bazie ${\cal B}$ :

$$[X]_{{\cal B}}=\left[\begin{array}{c}\langle X,u\rangle \langle X,v\rangle \langle X,w\rangle\end{array}\right].$$