next up previous
Up: Algebra liniowa II Previous: 14. Macierze symetryczne

15. Objętość w przestrzeni euklidesowej

W tym rozdziale zakładamy, że $(V,\langle\cdot,\cdot\rangle)$ jest przestrzenią euklidesową dowolnego wymiaru. Zdefiniujemy tu pojęcie objętości dla pewnych uogólnionych równoległościanów w przestrzeni $V$. Uzasadnimy też, że pojęcie to zgadza się z intuicjami dotyczącymi funkcji wyznacznika z początku rozdziału 5.

Załóżmy, że $v_1,\dots,v_n\in V$. Zbiór

\begin{displaymath}[v_1,\dots,v_n]=\left\{\sum_{i=1}^nt_iv_i:0\leq t_i\leq 1\right\}\end{displaymath}

nazywamy uogólnionym równoległościanem (lub kostką) rozpiętym przez wektory $v_1,\dots,v_n$.

Gdy wektory $v_1,\dots,v_n$ są liniowo niezależne i $V=E^n$, zbiór $[v_1,\dots,v_n]$ jest zwykłym równoległościanem (dla $n=3$) lub równoległobokiem (dla $n=2$) o wierzchołkach $O,v_1,\dots,v_n$.

Definicja 15.1   Definiujemy przez indukcję względem $n$ liczbę rzeczywistą $vol[v_1,\dots,v_n]$, zwaną ($n$-wymiarową) objętością uogólnionego równoległościanu $[v_1,\dots,v_n]$.
1) $vol[v_1]=\Vert v_1\Vert$.
2) Dla $n>1, vol[v_1,\dots,v_n]=vol[v_1,\dots,v_{n-1}]\cdot \Vert v_n-v_n'\Vert$, gdzie $v_n'$ jest rzutem prostopadłym wektora $v_n$ na podprzestrzeń $Lin(v_1,\dots,v_{n-1})$.

Zwróćmy uwagę, że rzut prostopadły na podprzestrzeń
$W=Lin(v_1,\dots,v_{n-1})$ istnieje, gdyż podprzestrzeń ta ma skończony wymiar, więc ma bazę ortonormalną (twierdzenie 11.1, uwaga 10.9). Ponadto liczba $\Vert v_n-v_n'\Vert$ to odległość wektora $v_n$ od podprzestrzeni $W$ (rozdział 11).

Fakt 15.2   1) Jeśli $v_1,\dots,v_n$ są liniowo zależne, to $vol[v_1,\dots,v_n]=0$.
2) Jeśli $v_1,\dots,v_n$ są liniowo niezależne, to

\begin{displaymath}vol[v_1,\dots,v_n]=\vert\det(A)\vert,\end{displaymath}

dla macierzy $A=[a_{ij}]_{n\times n}$, gdzie $a_{ij}=\langle b_i,v_j\rangle$, zaś zbiór ${\cal B}=\{b_1,\dots,b_n\}$ jest bazą ortonormalną przestrzeni $W=Lin(v_1,\dots,v_n)$.

Zwróćmy uwagę, że liczby $\langle b_i,v_j\rangle, i=1,\dots,k$ to współrzędne wektora $v_j$ w bazie ${\cal B}$ (uwaga 10.8).

Rozważmy szczególny przypadek, gdy $V=E^n$ i ${\cal B}={\cal E}$ jest standardową bazą ortonormalną. Wówczas kolumny macierzy $A$ w fakcie 15.2(2) to po prostu wektory $v_1,\dots,v_n$. Fakt ten potwierdza zatem naszą intuicję dotyczącą wyznacznika w rozdziale 5.
Dowód faktu 15.2. 1) Skoro $v_1,\dots,v_n$ są liniowo zależne, to dla pewnego $j\leq n$ wektor $v_j$ jest liniową kombinacją wektorów $v_1,\dots,v_{j-1}$. Dlatego jest on równy swojemu rzutowi $v_j'$ na podprzestrzeń $Lin(v_1,\dots,v_{j-1})$. Wtedy $\Vert v_j-v_j'\Vert=0$ i zgodnie z definicją 15.1,

\begin{displaymath}vol[v_1,\dots,v_j]=vol[v_1,\dots,v_{j-1}]\cdot\Vert v_j-v_j'\Vert=0,\end{displaymath}

skąd wynika, że również $vol[v_1,\dots,v_n]=0$.

2) Stosujemy indukcję względem $n$. Dla $n=1$ teza jest oczywista. Załóżmy, że $n>1$ i teza jest udowodniona dla $n-1$.

Niech $W'=Lin(v_1,\dots,v_{n-1})$. Zbiór ${\cal V}=\{v_1,\dots,v_n\}$ jest bazą przestrzeni $W$ i $A=m_{{\cal V}{\cal B}}(id)$. Zauważmy, że $\vert\det(A)\vert$ nie zależy od wyboru bazy ${\cal B}$ przestrzeni $W$. Istotnie, załóżmy, że ${\cal C}$ jest inną bazą ortonormalną przestrzeni $W$. Wtedy macierz $m_{{\cal B}{\cal C}}(id)$ jest ortogonalna, więc $\vert\det(m_{{\cal B}{\cal C}}(id)\vert=1$ (wniosek 11.13). Mamy $m_{{\cal V}{\cal C}}(id)=m_{{\cal B}{\cal C}}(id)\cdot A$, więc $\vert\det(m_{{\cal V}{\cal C}}(id))\vert=\vert\det(A)\vert$.

Stosując metodę ortonormalizacji Grama-Schmidta, możemy wybrać bazę ortonormalną ${\cal B}=\{b_1,\dots,b_n\}$ przestrzeni $W$ tak, że zbiór $\{b_1,\dots,b_{n-1}\}$ jest bazą przestrzeni $W'$. Niech $v_n'$ będzie rzutem prostopadłym wektora $v_n$ na przestrzeń $W'$.

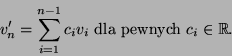
\begin{displaymath}v_n'=\sum_{i=1}^{n-1}c_iv_i\mbox{ dla pewnych }c_i\in {\mathbb{R}}.\end{displaymath}

$W=W'\oplus (W')^{\perp}$ (tu $(W')^{\perp}$ oznacza dopełnienie ortogonalne podprzestrzeni $W'$ w przestrzeni $W$). Dlatego $\dim(W')^{\perp}=1$.

Niech $A'=[a_{ij}']_{n\times n}$, gdzie

\begin{displaymath}a_{ij}=\langle b_i,v_j\rangle\mbox{ dla }j<n\mbox{ oraz }a'_{in}=\langle b_i,v_n-v_n'\rangle.\end{displaymath}

Dla $i,j<n, a'_{ij}=a_{ij}$, więc macierze

\begin{displaymath}A'_{n-1}=[a'_{ij}]_{(n-1)\times (n-1)}\mbox{ i } A_{n-1}=[a_{ij}]_{(n-1)\times (n-1)}\end{displaymath}

są równe. Z założenia indukcyjnego mamy

\begin{displaymath}\vert\det(A_{n-1})\vert=vol(v_1,\dots,v_{n-1}).\end{displaymath}

Ponadto $v_n-v_n',b_n\in (W')^{\perp}$, więc

\begin{displaymath}A'=\left[\begin{array}{ll}A_{n-1}&0\\ 0&a'_{nn}\end{array}\right]\mbox{ i } \det(A')=\det(A_{n-1})\cdot a'_{nn}.\end{displaymath}

Zauważmy, że $v_n-v'_n=sb_n$ dla pewnego $s\in {\mathbb{R}}$, więc

\begin{displaymath}\Vert v_n-v_n'\Vert=\vert s\vert\cdot\Vert b_n\Vert=\vert s\vert=\vert\langle b_n,v_n-v_n'\rangle\vert=\vert a'_{nn}\vert.\end{displaymath}

Dlatego

\begin{displaymath}\vert\det(A')\vert=\vert\det(A_{n-1})\vert\cdot\vert a'_{nn}\... ..._1,\dots,v_{n-1}]\cdot \Vert v_n-v_n'\Vert= vol(v_1,\dots,v_n).\end{displaymath}

Zapiszmy macierze $A$ i $A'$ jako ciągi kolumn. $A=(C_1,\dots,C_n),\ A'=(C_1',\dots,C_n')$. Zauważmy, że dla $j<n, C_j=C_j'$. Ponadto

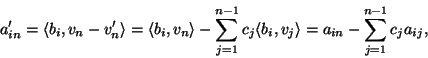
\begin{displaymath}a'_{in}=\langle b_i,v_n-v'_n\rangle=\langle b_i,v_n\rangle-\s... ...n-1}c_j\langle b_i,v_j\rangle=a_{in}-\sum_{j=1}^{n-1}c_ja_{ij},\end{displaymath}

więc $C_n'=C_n-\sum_{j=1}^{n-1}c_jC_j$. Dlatego

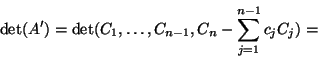
\begin{displaymath}\det(A')=\det(C_1,\dots,C_{n-1},C_n-\sum_{j=1}^{n-1}c_jC_j)=\end{displaymath}


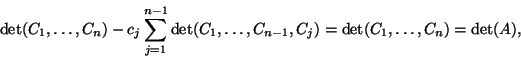
\begin{displaymath}\det(C_1,\dots,C_n)-c_j\sum_{j=1}^{n-1}\det(C_1,\dots,C_{n-1},C_j)=\det(C_1,\dots,C_n)=\det(A),\end{displaymath}

co kończy dowód.


Następny wniosek dostarcza innego sposobu obliczania objętości uogólnionego równoległościanu.

Wniosek 15.3   Załóżmy, że $v_1,\dots,v_n\in V$. Wtedy

\begin{displaymath}vol[v_1,\dots,v_n]=\sqrt{\det[\langle v_i,v_j\rangle]_{n\times n}}.\end{displaymath}

Dowód. Niech ${\cal B}$ będzie dowolną bazą ortonormalną przestrzeni $V$. Jeśli $v_1,\dots,v_n$ są liniowo zależne, to $vol[v_1,\dots,v_n]=0$ i macierz $[\langle v_i,v_j\rangle]$ ma wyznacznik $0$ (gdyż jej kolumny są liniowo zależne). W tym przypadku wniosek jest więc udowodniony.

Załóżmy więc, że $v_1,\dots,v_n$ są liniowo niezależne. Niech $\{b_1,\dots,b_n\}$ będzie bazą ortonormalną przestrzeni $Lin(v_1,\dots,v_n)$ i niech $a_{ij}=\langle b_i,v_j\rangle$. Na mocy uwagi 10.8 i faktu 15.2 mamy

\begin{displaymath}v_j=\sum_{i=1}^na_{ij}b_i\mbox{ i }vol[v_1,\dots,v_n]=\vert\det[a_{ij}]\vert.\end{displaymath}


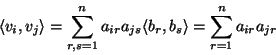
\begin{displaymath}\langle v_i,v_j\rangle=\sum_{r,s=1}^na_{ir}a_{js}\langle b_r,b_s\rangle=\sum_{r=1}^na_{ir}a_{jr}\end{displaymath}

Dlatego $[\langle v_i,v_j\rangle]_{n\times n}=[a_{ij}]_{n\times n}\cdot[a_{ij}]_{n\times n}^*$ i

\begin{displaymath}\det[\langle v_i,v_j\rangle ]=\det[a_{ij}]\cdot\det[a_{ij}]^*=\det[a_{ij}]^2=(vol[v_1,\dots,v_n])^2.\end{displaymath}


Wyznacznik $\det[\langle v_i,v_j\rangle]_{n\times n}$ występujący we wniosku 15.3 nazywamy wyznacznikem Grama układu wektorów $v_1,\dots,v_n$.

Wniosek 15.4   Załóżmy, że $\dim(V)=n$ i $F:V\rightarrow V$ jest liniowe. Wtedy $F$ zmienia $n$-wymiarową objętość w stodunku $\vert\det(F)\vert$, tzn.

\begin{displaymath}vol(F[R])=\vert\det(F)\vert\cdot vol(R)\end{displaymath}

dla każdego uogólnionego równoległościanu $R=[v_1,\dots,v_n]$.

Dowód. Podobnie, jak w dowodzie poprzedniego wniosku, możemy założyć, że wektory $v_1,\dots,v_n$ są liniowo niezależne. Macierz $([F(v_1)]_{{\cal B}},\dots,[F(v_n)]_{{\cal B}})$ jest równa iloczynowi macierzy $m_{{\cal B}}(F)\cdot([v_1]_{{\cal B}},\dots,[v_n]_{{\cal B}})$, dlatego

\begin{displaymath}vol(F[R])=\vert\det([F(v_1)]_{{\cal B}},\dots,[F(v_n)]_{{\cal B}})\vert=\end{displaymath}


\begin{displaymath}\vert\det(m_{{\cal B}}(F)\vert\cdot\vert\det([v_1]_{{\cal B}},\dots,[v_n]_{{\cal B}})\vert=\vert\det(F)\vert\cdot vol(R).\end{displaymath}


next up previous
Up: Algebra liniowa II Previous: 14. Macierze symetryczne
Ludomir Newelski 2005-09-21