3. Bazy i przekształcenia liniowe

Każdy wektor $X\in {\mathbb{R}}^n$ jest kolumną składającą się ze współrzędnych $x_1,\dots x_n$ wektora $X$. Współrzędne te spełniaja równość

$$X=x_1E_1+x_2E_2+\cdots+x_nE_n,$$

w której występują wektory standardowej bazy ${\mathbb{R}}^n$. W podobny sposób możemy zdefiniować współrzędne dowolnego wektora przestrzeni liniowej $V$ względem ustalonej bazy ${\cal B}$ tej przestrzeni. Mówi o tym poniższa uwaga.

Uwaga 3.1   Załóżmy, że ${\cal B}=\{b_1,b_2,\dots,b_n\}$ jest bazą przestrzeni $V$. Wówczas dla każdego wektora $v\in V$ istnieje dokładnie jeden ciąg $(t_1,\dots,t_n)\in {\mathbb{R}}^n$ taki, że

$$(*) v=t_1b_1+t_2b_2+\dots+t_nb_n.$$

Ciąg ten nazywamy ciągiem współrzędnych wektora $v$ w bazie ${\cal B}$. Piszemy wówczas

$$[v]_{{\cal B}}=\left[\begin{array}{l}t_1 t_2\\ \vdots t_n\end{array}\right].$$

Czasami dla wygody zapisujemy $[v]_{{\cal B}}$ w postaci wiersza zamiast kolumny.
Dowód. Skoro ${\cal B}$ jest bazą $V$, to wektor $v$ jest liniową kombinacją wektorów z ${\cal B}$, zatem dla pewnych $t_1,\dots,t_n\in {\mathbb{R}}$ możemy go przedstawić w postaci $(*)$. Pokażemy teraz, że to przedstawienie jest jednoznaczne.

Przypuśćmy, że

$$(**) v=t_1'b_1+t_2'b_2+\cdots+t_n'b_n$$

dla pewnych $t_1',\dots,t_n'\in {\mathbb{R}}$. Wystarczy pokazać, że $t_i=t_i'$ dla wszystkich $i$. Odejmując stronami równości $(*)$ i $(**)$ dostajemy

$$O=v-v=(t_1-t_1')b_1+(t_2-t_2')b_2+\cdots+(t_n-t_n')b_n.$$

Zbiór ${\cal B}$, jako baza, jest liniowo niezależny, więc z faktu 2.3 wynika, że $0=t_i-t_i'$, czyli $t_i=t_i'$ dla wszystkich $i$, czego należało dowieść.

Przykład.

Rozważmy bazę standardową ${\cal E}=\{E_1,\dots,E_n\}$ przestrzeni ${\mathbb{R}}^n$. Niech $X\in {\mathbb{R}}^n$, to znaczy

$$X=\left[\begin{array}{c}x_1 x_2 \vdots x_n\end{array}\right],$$

również $X=x_1E_1+\cdots+x_nE_n$. Widzimy więc, że $x_1,\dots,x_n$ to współrzędne wektora $X$ w bazie ${\cal E}$

$$[X]_{{\cal E}}=\left[\begin{array}{c}x_1 x_2 \vdots\\ x_n\end{array}\right].$$

W definicji układu współrzędnych wektora $v\in V$ w bazie ${\cal B}$ istotna jest numeracja $b_1,\dots,b_n$ (uporządkowanie) wektorów bazy ${\cal B}$. Istotnie, rozważmy standardową bazę ${\mathbb{R}}^n$ ze zmienioną kolejnością wektorów, np. niech ${\cal E}'=\{E_n,E_{n-1},\dots,E_1\}$. Wówczas

$$[X]_{{\cal E}'}=\left[\begin{array}{c}x_n x_{n-1} \vdots\\ x_1\end{array}\right].$$

Kontynuując analizę przestrzeni ${\mathbb{R}}^n$ rozważmy podprzestrzenie $V_i=Lin(E_i)$, $i=1,\dots,n$. Wówczas

$$V_1+\cdots +V_n={\mathbb{R}}^n,$$

bo każdy wektor $X\in {\mathbb{R}}^n$ można przedstawić w postaci

$$X=x_1E_1+\cdots+x_nE_n$$

i wektory $x_iE_i$ leżą w podprzestrzeniach $V_i$. Ponadto przedstawienie $X$ w postaci sumy wektorów z podprzestrzeni $V_i$ jest jednoznaczne (bo ${\cal E}$ jest bazą). W tej sytuacji piszemy

$${\mathbb{R}}^n=V_1\oplus V_2\oplus\cdots\oplus V_n$$

i mówimy, że ${\mathbb{R}}^n$ jest sumą prostą przestrzeni $V_1,\dots.V_n$.

Ogólniej, załóżmy, że $V_1,\dots,V_n$ są podprzestrzeniami przestrzeni $V$.

Definicja 3.2   $V$ jest sumą prostą podprzestrzeni $V_1,\dots,V_n\iff$ każdy wektor $v\in V$ można jednoznacznie przedstawić w postaci

$$v=v_1+v_2+\cdots+v_n,$$

gdzie $v_1\in V_1,\dots,v_n\in V_n$.
Fakt, że $V$ jest sumą prostą podprzestrzeni $V_1\dots,V_n$, zapisujemy symbolicznie w postaci $V=V_1\oplus\cdots\oplus V_n$.

Rysunek: $\mathbb{R}^3=P\oplus L$

Uwaga 3.3   1) Jeśli $V=V_1+V_2$, to $\dim(V)\leq\dim(V_1)+\dim(V_2)$.
2) Jeśli $V=V_1\oplus V_2$, to $\dim(V)=\dim(V_1)+\dim(V_2)$.
3) Ogólniej, jeśli $V=V_1\oplus\cdots\oplus V_n$, to $\dim(V)=\dim(V_1)+\cdots+\dim(V_n)$.

Dowód. Niech ${\cal B}_1$ będzie bazą $V_1$, zaś ${\cal B}_2$ bazą $V_2$.

1) ${\cal B}_1\cup {\cal B}_2$ generuje $V_1+V_2$, więc gdy $V=V_1+V_2$, to zbiór ${\cal B}_1\cup {\cal B}_2$ generuje $V$, więc zawiera pewną bazę przestrzeni $V$. Dlatego

$$\dim(V)\leq\vert{\cal B}_1\cup {\cal B}_2\vert\leq\vert{\cal B}_1\vert+\vert{\cal B}_2\vert=\dim(V_1)+\dim(V_2).$$

2) Załóżmy, że $V=V_1\oplus V_2$. Pokażemy, że zbiór ${\cal B}_1\cup {\cal B}_2$ jest bazą przestrzeni $V$. Na mocy dowodu (1), zbiór ten generuje $V$. Wystarczy więc pokazać, że jest on liniowo niezależny.

Przypuśćmy, że

$$\sum_it_ib_i+\sum_jt'_jb'_j=O$$

dla pewnych $t_i,t'_j\in {\mathbb{R}}$ i $b_i\in B_1, b'_j\in B_2$. Wystarczy pokazać, że wszystkie skalary $t_i,t'_j$ są równe $0$.

Niech

$$v_1=\sum_it_ib_i, v_2=\sum_jt'_jb'_j.$$

Wówczas $v_1\in V_1, v_2\in V_2$ oraz $v_1+v_2=O$. Z drugiej strony wektor $O$ możemy przedstawić w postaci $O+O=O$ i $O$ leży w obu przestrzeniach $V_1,V_2$. Jednak przedstawienie wektora $O$ w postaci sumy wektorów z $V_1$ i $V_2$ jest jednoznaczne, dlatego wnioskujemy, ze $v_1=O$ oraz $v_2=O$. Korzystając z tego, że ${\cal B}_1$ i ${\cal B}_2$ są bazami przestrzeni $V_1,V_2$ odpowiednio, dostajemy, że wszystkie skalary $t_i,t'_j$ są równe $0$.

Dowód (3) jest podobny.

Fakt 3.4   Jeśli $V_1$ jest podprzestrzenią $V$, to istnieje podprzestrzeń $V_2\subset V$ taka, że $V_1\oplus V_2=V$.

Dowód. Niech ${\cal B}_1$ będzie bazą $V_1$. Na mocy twierdzenia 2.5 istnieje baza ${\cal B}$ przestrzeni $V$, zawierająca ${\cal B}_1$. łatwo sprawdzić, że podprzestrzeń $V_2=Lin({\cal B}\setminus {\cal B}_1)$ spełnia nasze żądania.

Podprzestrzeń $V_2$ z faktu 3.4 nazywamy podprzestrzenią dopełniczą podprzestrzeni $V_1$ w przestrzeni $V$. Podprzestrzeń tę można wybrać na wiele sposobów. Na przykład, gdy $V={\mathbb{R}}^2$ i $V_1\subset {\mathbb{R}}^2$ jest prostą przechodzącą przez $O$, to podprzestrzenią dopełniczą do $V_1$ w ${\mathbb{R}}^2$ będzie każda prosta przechodząca przez $O$, różna od $V_1$.

Załóżmy, że przestrzeń $V$ ma wymiar $n$ i ${\cal B}$ jest bazą $V$. Wówczas dowolny wektor $v\in V$ jest wyznaczony jednoznacznie przez układ swoich współrzędnych w bazie ${\cal B}$, który to układ jest pewnym wektorem przestrzeni ${\mathbb{R}}^n$. W ten sposób dostajemy pewną wzajemnie jednoznaczną odpowiedniość miedzy wektorami przestrzeni $V$ i wektorami przestrzeni ${\mathbb{R}}^n$. Okazuje się, że odpowiedniość ta jest przykładem izomorfizmu przestrzeni liniowych.

Definicja 3.5   Załóżmy, że $V,W$ są dwiema przestrzeniami liniowymi nad ${\mathbb{R}}$. Mówimy, że funkcja $F:V\rightarrow W$ jest izomorfizmem liniowym, gdy spełnione są następujące warunki.
1) $F$ jest 1-1 i ``na'' (tzn. $F$ jest bijekcją).
2) $\forall v_1,v_2\in V, F(v_1+v_2)=F(v_1)+F(v_2)$.
3) $\forall t\in {\mathbb{R}} \forall v\in V, F(tv)=tF(v)$.

Gdy taki izomorfizm istnieje, mówimy, że $V$ i $W$ są izomorficzne (symbolicznie $V\cong W$).

Działania dodawania wektorów i mnożenia wektorów przez skalary występujące po lewej stronie równości w warunkach (2),(3) definicji 3.5 odnoszą się do przestrzeni $V$, działania występujące po prawej stronie tych równości odnoszą się do przestrzeni $W$.

Gdy w definicji 3.5 zastąpimy ciało ${\mathbb{R}}$ innym ciałem $K$, dostaniemy pojęcie izomorfizmu przestrzeni liniowych nad $K$. Pojęcie to jest szczególnym przypadkiem pojęcia izomorfizmu dowolnych struktur algebraicznych. łatwo sprawdzić, że
a) identyczność $id:V\rightarrow V$ jest izomorfizmem,
b) funkcja odwrotna do izomorfizmu jest izomorfizmem, jak również
c) złożenie izomorfizmów jest izomorfizmem.
Stąd wynika wprost, że izomorficzność jest relacją równoważności w klasie przestrzeni liniowych nad ${\mathbb{R}}$.

Izomorficzne struktury algebraiczne mają te same algebraiczne własności, są nieodróżnialne z punktu widzenia algebry. W szczególności izomorficzne przestrzenie liniowe mają ten sam wymiar (ćwiczenie). Okazuje sie, że na odwrót przestrzenie tego samego wymiaru są izomorficzne. Wynika to z następującego twierdzenia o izomorfizmie przestrzeni liniowych.

Twierdzenie 3.6 (o izomorfizmie liniowym)   Jeśli $\dim(V)=n$, to istnieje izomorfizm liniowy $F:V\rightarrow {\mathbb{R}}^n$.

Dowód. Niech ${\cal B}=\{b_1,\dots,b_n\}$ będzie pewną bazą $V$. Definiujemy $F:V\rightarrow {\mathbb{R}}^n$ wzorem

$$F(v)=[v]_{{\cal B}},$$

to znaczy $F(v)$ jest układem współrzędnych wektora $v$ w bazie ${\cal B}$. Pokażemy, że $F$ jest izomorfizmem. Z dyskusji przed definicją 3.5 wynika, że $F$ jest bijekcją. Wystarczy zatem sprawdzić warunki (2) i (3) definicji 3.5.

(2) Dla $v,w\in V, F(v+w)=F(v)+F(w)$.
Istotnie, załóżmy, że

$$F(v)=[v]_{{\cal B}}=\left[\begin{array}{c}t_1 \vdots t_n\... ...B}}=\left[\begin{array}{c}s_1 \vdots s_n\end{array}\right].$$

Znaczy to, że $v=\sum t_ib_i, w=\sum s_ib_i$. Wówczas $v+w=\sum(t_i+s_i)b_i$, zatem

$$F(v+w)=[v+w]_{{\cal B}}=\left[\begin{array}{c}t_1+s_1 \vdots\\ t_n+s_n\end{array}\right].$$

Widzimy, że $F(v+w)=F(v)+F(w)$.

Warunek $F(tv)=tF(v)$ sprawdzamy podobnie.

Wniosek 3.7   Przestrzenie tego samego wymiaru są izomorficzne.

Dowód. Dowód przeprowadzimy w przypadku przestrzeni wymiaru skończonego. Załóżmy, że $V,W$ są przestrzeniami liniowymi wymiaru $n$. Na mocy twierdzenia 3.6 istnieją izomorfizmy $F:V\rightarrow {\mathbb{R}}^n$ i $G:W\rightarrow {\mathbb{R}}^n$. łatwo sprawdzić, że funkcja $G^{-1}\circ F: V\rightarrow W$ jest izomorfizmem.

Przykład.

Niech

$$b_1=\left[\begin{array}{c}0 1\\ 1\end{array}\right],b_2=\l... ...\begin{array}{c}1 0\\ 1\end{array}\right]\in {\mathbb{R}}^3.$$

Wektory $b_1,b_2,b_3$ są liniowo niezależne oraz $\dim({\mathbb{R}}^3)=3$, więc zbiór ${\cal B}=\{b_1,b_2,b_3\}$ jest bazą ${\mathbb{R}}^3$.

Niech

$$u=\left[\begin{array}{c}1 1 1\end{array}\right].$$

Współrzędne $u$ w bazie standardowej to

$$[u]_{{\cal E}}= \left[\begin{array}{c}1 1 1\end{array}\right] .$$

Znajdziemy współrzędne $u$ w bazie ${\cal B}$. Są to jedyne liczby $t_1,t_2,t_3$ takie, że

$$\left[\begin{array}{c}1 1\\ 1\end{array}\right]=t_1b_1+t_2... ...[\begin{array}{c}t_2+t_3 t_1+t_2 t_1+t_3\end{array}\right].$$

Zatem liczby $t_1,t_2,t_3$ spełniają równości

$$\left\{\begin{array}{ccccc}t_1&+&t_3&=&1 t_1&+&t_2&=& 1 t_1&+&t_3&=& 1\end{array}\right.,$$

skąd dostajemy $t_1=t_2=t_3=\frac{1}{2}$. Zatem

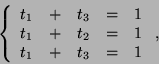
$$[u]_{{\cal B}}=\left[\begin{array}{c}1/2 1/2\\ 1/2\end{array}\right].$$

Zauważmy też, że wektor $u$ ma również te same współrzędne w innej bazie

$${\cal B}'=\left\{\left[\begin{array}{c}2 0\\ 0\end{array}\... ...ht],\left[\begin{array}{c}0 0\\ 2\end{array}\right]\right\}.$$

Izomorfizm przestrzeni liniowych jest szczególnym przypadkiem przekształcenia liniowego. Z przekształceniami liniowymi czytelnik spotkał się już w przypadku przestrzeni ${\mathbb{R}}^n$.

$$(*) F:{\mathbb{R}}^n\rightarrow {\mathbb{R}}^m\mbox{ jest liniowe}\iff F(X)=AX$$

dla pewnej macierzy $A=[a_{ij}]_{m\times n}$ o $m$ wierszach i $n$ kolumnach (tzn. wymiaru $m\times n$).

Wektor w ${\mathbb{R}}^n$ jest kolumną liczb wysokości $n$, ma więc sens mnożenie wektora przez macierz. W przypadku abstrakcyjnych przestrzeni liniowych trudno mówić o mnożeniu wektora przez macierz, gdyż rolę wektorów mogą odgrywać zupełnie dowolne obiekty. Dlatego pojęcie przekształcenia liniowego dowolnych przestrzeni liniowych $V,W$ definiujemy inaczej.

Definicja 3.8   $F:V\rightarrow W$ jest przekształceniem liniowym, gdy zachodzą następujące warunki.
1) (addytywność) $\forall v_1,v_2\in V, F(v_1+v_2)=F(v_1)+F(v_2)$.
2) (jednorodność) $\forall t\in R \forall v\in V, F(tv)=tF(v)$.

Warunki te pojawiły się już w definicji izomorfizmu przestrzeni liniowych. Izomorfizm liniowy jest to więc przekształcenie liniowe, które dodatkowo jest bijekcją, to znaczy jest odwracalne. Definicja 3.8 zgadza sie również z definicją macierzową przekształcenia liniowego przestrzeni ${\mathbb{R}}^n$, każde bowiem przekształcenie przestrzeni ${\mathbb{R}}^n$ zadane wzorem $(*)$ jest addytywne i jednorodne.

Przekształcenia liniowe są blisko związane ze strukturą przestrzeni liniowych. Oznaczmy przez $O_V,O_W$ wektory zerowe w przestrzeniach $V,W$ odpowiednio.

Uwaga 3.9   1) Jeśli $F:V\rightarrow W$ jest liniowe, to $F(O_V)=O_W$, $F(-v)=-F(v)$ dla każdego wektora $v\in V$ oraz ogólniej $F(\sum t_iv_i)=\sum t_iF(v_i)$.
2) Złożenie przekształceń liniowych jest liniowe.

Dowód. (1) $F(-v)=F((-1)v)=(-1)F(v)=-F(v)$.
$F(O_V)=F(v+(-v))=F(v)+(-F(v))=O_W$. Równość $F(\sum t_iv_i)=\sum t_iF(v_i)$ wynika łatwo z addytywności i jednorodności $F$.

(2) Załóżmy, że $V,W,U$ są przestrzeniami liniowymi oraz $F:V\rightarrow W, G:W\rightarrow U$ są liniowe. łatwo sprawdzić, że wówczas złożenie $G\circ F:V\rightarrow U$ jest addytywne i jednorodne, więc liniowe.

Przykłady przekształceń liniowych.

1. Przekształcenie zerowe $O:V\rightarrow W$ dane wzorem $O(v)=O_W$. Przekształcenie identycznościowe $id:V\rightarrow V$ dane wzorem $id(v)=v$.

2. Dylatacja $D_t:V\rightarrow V$ o skali $t\in {\mathbb{R}}$, dana wzorem $D_t(v)=tv$.

3. Niech $a_1,\dots,a_k\in {\mathbb{R}}$. Wówczas przekształcenie $F:C({\mathbb{R}})\rightarrow {\mathbb{R}}^k$ dane wzorem $F(f)=(f(a_1),\dots,f(a_k))$ jest liniowe.

4. Przekształcenie $F:{\mathbb{R}}[X]\rightarrow {\mathbb{R}}[X]$ dane wzorem $F(W)=W'$, gdzie $W'$ to pochodna wielomianu $W$.

5. Szczególnym przypadkiem są przekształcenia liniowe $F:V\rightarrow {\mathbb{R}}$. (${\mathbb{R}}$ jest jednowymiarową przestrzenią liniową.) Przekształcenia takie nazywamy funkcjonałami liniowymi. Przekształcenie z przykładu 3 jest funkcjonałem liniowym dla $k=1$. Inny przykład to przekształcenie $G:C({\mathbb{R}})\rightarrow {\mathbb{R}}$ dane wzorem $G(f)=\int_0^1f(x)dx$.

Załóżmy teraz, że ${\cal B}=\{b_1,\dots,b_n\}$ i ${\cal C}=\{c_1,\dots,c_m\}$ są bazami przestrzeni $V$ i $W$ odpowiednio. Niech $A=[a_{ij}]_{m\times n}$ będzie dowolną macierzą wymiaru $m\times n$. Definiujemy wówczas przekształcenie $F:V\rightarrow W$ wzorem

$$(**) F(v)=w\iff A[v]_{{\cal B}}=[w]_{{\cal C}}.$$

łatwo sprawdzić, że tak zdefiniowane przekształcenie jest liniowe. Okazuje się, że wszystkie przekształcenia liniowe $V\rightarrow W$ powstają w ten sposób.

Twierdzenie 3.10   $F:V\rightarrow W$ jest liniowe $\iff$ dla pewnej macierzy $A$ wymiaru $m\times n$ zachodzi $(**)$.

Dowód. Dowód jest w istocie ten sam, co dla przekształceń liniowych ${\mathbb{R}}^n\rightarrow {\mathbb{R}}^m$. $\Leftarrow$ jest łatwe.

$\Rightarrow.$ Załóżmy, że $F:V\rightarrow W$ jest liniowe. Wektory współrzędnych $[F(b_1)]_{{\cal C}},\dots,[F(b_n)]_{{\cal C}}$ mają wysokość $m$. Niech

$$\left[\begin{array}{c}a_{1j} a_{2j} \vdots a_{mj}\end{array}\right]=[F(b_j)]_{{\cal C}}.$$

Niech $A$ będzie macierzą $m\times n$ o kolumnach $[F(b_1)]_{{\cal C}},\dots,[F(b_n)]_{{\cal C}}$, tzn. $A=([F(b_1)]_{{\cal C}},\dots,[F(b_n)]_{{\cal C}})=[a_{ij}]_{m\times n}$. Pokażemy, że macierz $A$ spełnia $(**)$. W tym celu wystarczy sprawdzić, że dla dowolnego wektora $v\in V$ mamy $[F(v)]_{{\cal C}}=A[v]_{{\cal B}}$. Niech

$$\left[\begin{array}{c}x_1 x_2 \vdots\\ x_n\end{array}\right]=[v]_{{\cal B}}.$$

Wówczas

$$[F(v)]_{{\cal C}}=[F(x_1b_1+\cdots+x_nb_n)]_{{\cal C}}=[x_1F(b_1)+\cdots+x_nF(b_n)]_{{\cal C}}=$$

$$=x_1[(F(b_1)]_{{\cal C}}+\cdots+x_n[F(b_n)]_{{\cal C}}=x_1\le... ...{array}{c}a_{1n}\\ a_{2n} \vdots a_{mn}\end{array}\right]=$$

$$=[a_{ij}]_{m\times n}\left[\begin{array}{c}x_1 x_2 \vdots\\ x_n\end{array}\right]=A[v]_{{\cal B}}.$$

Macierz $A$ z twierdzenia 3.10 nazywamy macierzą przekształcenia $F$ w bazach ${\cal B},{\cal C}$. Macierz tę oznaczamy przez $A=m_{{\cal B}{\cal C}}(F)$. Zauważmy, że kolumny macierzy $m_{{\cal B}{\cal C}}(F)$ są to układy współrzędnych w bazie ${\cal C}$ obrazów względem $F$ kolejnych wektorów bazy ${\cal B}$. W przypadku, gdy $F:V\rightarrow V$, piszemy $m_{{\cal B}}(F)$ zamiast $m_{{\cal B}{\cal B}}(F)$. Macierz $m_{{\cal B}}(F)$ nazywamy macierzą przekształcenia $F$ w bazie ${\cal B}$.

Przykłady.

1. Dla przekształcenia $F:{\mathbb{R}}^n\rightarrow {\mathbb{R}}^m$ zdefiniowanego wzorem $(*)$ macierz $A$ występująca w tym wzorze jest macierzą przekształcenia $F$ w bazach standardowych ${\cal E}\subset {\mathbb{R}}^n,{\cal E}'\subset {\mathbb{R}}^m$. Możemy więc napisać $A=m_{{\cal E}{\cal E}'}(F)$. W przypadku baz standardowych opuszczamy zazwyczaj indeksy ${\cal E},{\cal E}'$ pisząc $A=m(F)$.

2. Określamy przekształcenie liniowe $F:{\mathbb{R}}_3[X]\rightarrow {\mathbb{R}}_3[X]$ wzorem $F(W)$ $= W'+W(0)$. Rozważmy bazy ${\cal B}=\{1,X,X^2,X^3\}, {\cal C}=\{X^3, X^2, X, 1 \}$ przestrzeni ${\mathbb{R}}_3[X]$. Znajdziemy macierz $m_{{\cal B}{\cal C}}(F)$. W tym celu obliczamy współrzędne w bazie ${\cal C}$ obrazów wektorów bazy ${\cal B}$ względem $F$.

$$F(1)=1, F(X)=1, F(X^2)=2X, F(X^3)=3X^2.$$

Zatem

$$[F(1)]_{{\cal C}}=\left[\begin{array}{c}0 0 0 1\end{arr... ...\cal C}}=\left[\begin{array}{c}0 0 0 1\end{array}\right],$$

$$[F(X^2)]_{{\cal C}}=\left[\begin{array}{c}0 0 2 0\end{a... ...\cal C}}=\left[\begin{array}{c}0 3 0 0\end{array}\right].$$

Dlatego

$$m_{{\cal B}{\cal C}}(F)=\left[\begin{array}{cccc}0&0&0&0 0&0&0&3 0&0&2&0\\ 1&1&0&0\end{array}\right].$$

Znając macierz przekształcenia $F:V\rightarrow W$ w danych bazach możemy łatwo obliczać obrazy wektorów względem $F$.

Mnożenie macierzy jest ścisłe związane ze składaniem przekształceń liniowych ${\mathbb{R}}^n\rightarrow {\mathbb{R}}^m$. Podobny związek występuje ze składaniem przekształceń liniowych abstrakcyjnych przestrzeni liniowych.

Załóżmy, że $V,W,U$ są przestrzeniami liniowymi o skończonych bazach ${\cal B},{\cal C},{\cal D}$ odpowiednio. Załóżmy, że $F:V\rightarrow W, G:W\rightarrow U$ są liniowe oraz

$$H=G\circ F:V\rightarrow U$$

jest złożeniem $F$ i $G$. Na mocy uwagi 3.9, przekształcenie $H$ jest liniowe. Twierdzenie 3.11 wyjaśnia związek miedzy macierzami przekształceń $F,G$ i $H$.

Twierdzenie 3.11   $m_{{\cal B}{\cal D}}(H)=m_{{\cal C}{\cal D}}(G)\cdot m_{{\cal B}{\cal C}}(F)$.

Dowód. Niech $v$ będzie dowolnym wektorem z $V$. Wówczas korzystając z definicji macierzy przekształcenia liniowego mamy

$$m_{{\cal B}{\cal D}}(H)[v]_{{\cal B}}=[H(v)]_{{\cal D}}=[G(F(v))]_{{\cal D}}=m_{{\cal C}{\cal D}}(G)[F(v)]_{{\cal C}}=$$

$$=m_{{\cal C}{\cal D}}(G)(m_{{\cal B}{\cal C}}(F)[v]_{{\cal B}... ...cal C}{\cal D}}(G)\cdot m_{{\cal B}{\cal C}}(F))[v]_{{\cal B}}.$$

Wektor $[v]_{{\cal B}}$ możemy traktować jako macierz wymiaru $n\times 1$. Ostatnia równość w powyższym ciągu równości wynika więc z łączności mnożenia macierzy.

Gdy $v$ przebiega $V$, wektory $[v]_{{\cal B}}$ przebiegają całą przestrzeń ${\mathbb{R}}^n$ (na mocy twierdzenia 3.6). Dlatego widzimy, że dla dowolnego wektora $X\in {\mathbb{R}}^n$ mamy

$$m_{{\cal B}{\cal D}}(H)\cdot X=(m_{{\cal C}{\cal D}}(G)\cdot m_{{\cal B}{\cal C}}(F))\cdot X.$$

Podstawiając w tej równości za $X$ wektor bazowy $E_i$ dostajemy po obu stronach równości $i$-te kolumny macierzy $m_{{\cal B}{\cal D}}(H)$ i $m_{{\cal C}{\cal D}}(G)m_{{\cal B}{\cal C}}(F)$. Dlatego te macierze są równe.