12. Arytmetyka liczb kardynalnych

Liczby kardynalne (moce zbiorów) oznaczamy zazwyczaj małymi gotyckimi literami ${\mathfrak{m}},{\mathfrak{n}}$ lub greckimi $\kappa,\mu$, chyba że dana liczba ma specjalne oznaczenie, jak na przykład $\aleph_0,{\mathfrak{c}}$.

Definicja 12.1 (1)   Suma ${\mathfrak{m}}+{\mathfrak{n}}$ liczb kardynalnych ${\mathfrak{m}},{\mathfrak{n}}$ jest to moc zbioru $A\cup B$, gdzie ${\mathfrak{m}}=\vert A\vert, {\mathfrak{n}}=\vert B\vert$ i zbiory $A,B$ są rozłączne.
(2) Iloczyn ${\mathfrak{m}}\cdot{\mathfrak{n}}$ liczb ${\mathfrak{m}},{\mathfrak{n}}$ to moc zbioru $A\times B$, gdzie ${\mathfrak{m}}=\vert A\vert, {\mathfrak{n}}=\vert B\vert$.
(3) ${\mathfrak{n}}$-ta potęga liczby ${\mathfrak{m}}$, oznaczana przez ${\mathfrak{m}}^{{\mathfrak{n}}}$, to moc zbioru $A^B$ wszystkich funkcji $f:B\to A$.

Jasne jest, że definicje te nie zależą od wyboru zbiorów $A$ i $B$. Jeśli mamy ${\mathfrak{m}}=\vert A\vert, {\mathfrak{n}}=\vert B\vert$, to łatwo uzyskać zbiory $A'\sim A$ i $B'\sim B$, które dodatkowo są rozłączne. Mianowicie niech $a\neq b$. Wówczas możemy przyjąc $A'=\{a\}\times A$ i $B'=\{b\}\times B$. Widzimy, że bez kłopotu w punkcie (1) powyższej definicji znajdziemy odpowiednie zbiory $A,B$. Zwróćmy uwagę, że w przypadku, gdy liczby ${\mathfrak{m}}$ i ${\mathfrak{n}}$ są skończone (czyli są liczbami naturalnymi), to suma, iloczyn i odpowiednia potęga będą liczbami naturalnymi równymi zwykłej sumie, iloczynowi i potędze liczb naturalnych.

Łatwo pokazać, że dodawanie i mnożenie liczb kardynalnych są przemienne i łączne oraz mnożenie jest rozdzielne względem dodawania. Definicja potęgowania liczb kardynalnych jest naturalna. Istotnie, niech ${\mathfrak{m}}=\vert A\vert$, zaś ${\mathfrak{n}}=\vert B\vert$. Wówczas funkcję $f:B\to A$ możemy traktować jak uogólniony ciąg $(a_x)_{x\in B}$, gdzie $a_x=f(x)$ i zbiór $A^B$ to uogólniona potęga kartezjańska $\vert B\vert$ kopii zbioru $A$ (porównaj rozdział 10).

Znaczenie operacji potęgowania wyjaśnia następująca uwaga.

Uwaga 12.2   $\vert{\cal P}(X)\vert=2^{\vert X\vert}$.

Dowód. $2^{\vert X\vert}$ to moc zbioru $\{0,1\}^X$ wszystkich funkcji $f:X\to\{0,1\}$. Wystarczy więc pokazać, że zbiory ${\cal P}(X)$ i $\{0,1\}^X$ są równoliczne.

Dla zbioru $A\subseteq X$ definiujemy funkcje $\chi_A:X\to\{0,1\}$ wzorem

$$\chi_A(x)=\left\{\begin{array}{cc}0,&\mbox{ gdy }x\not\in A\\ 1,&\mbox{ gdy }x\in A\end{array}\right..$$

Funkcję $\chi_A$ nazywamy funkcją charakterystyczną zbioru $A$. Łatwo stwierdzić, że przypisanie zbiorowi $A\subseteq X$ jego funkcji charakterystycznej jest bijekcją między zbiorem ${\cal P}(X)$ i $\{0,1\}^X$, co kończy dowód. $\Box$

Korzystając z wyników z poprzedniego rozdziału, dla każdej liczby naturalnej $n>0$ dostajemy

$$\aleph_0+\aleph_0=\aleph_0\cdot\aleph_0=\aleph_0+n=\aleph_0\cdot n=\aleph_0^n=\aleph_0,$$

$${\mathfrak{c}}+{\mathfrak{c}}={\mathfrak{c}}\cdot{\mathfrak{c... ...ak{c}}+n={\mathfrak{c}}\cdot n={\mathfrak{c}}^n={\mathfrak{c}}.$$

Korzystamy tu z tego, że ${\mathfrak{m}}^n=\underbrace{{\mathfrak{m}}\cdot\dots\cdot{\mathfrak{m}}}_n$.

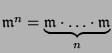Liczby kardynalne możemy też porównywać.

Definicja 12.3 (1)   ${\mathfrak{m}}\leq {\mathfrak{n}}\Leftrightarrow$ pewien zbiór $A$ mocy ${\mathfrak{n}}$ zawiera podzbiór mocy ${\mathfrak{m}}$.
(2) Gdy ${\mathfrak{m}}\leq{\mathfrak{n}}$ i ${\mathfrak{m}}\neq{\mathfrak{n}}$, piszemy ${\mathfrak{m}}<{\mathfrak{n}}$.

Uwaga 12.4 (1)   Jeśli pewien zbiór mocy ${\mathfrak{n}}$ zawiera podzbiór mocy ${\mathfrak{m}}$, to każdy zbiór mocy ${\mathfrak{n}}$ zawiera podzbiór mocy ${\mathfrak{m}}$.
(2) (przechodniość $\leq$) Jeśli ${\mathfrak{m}}\leq{\mathfrak{n}}$ i ${\mathfrak{n}}\leq\kappa$, to ${\mathfrak{m}}\leq\kappa$.
(3) (antysymetryczność $\leq$) Jeśli ${\mathfrak{m}}\leq{\mathfrak{n}}$ i ${\mathfrak{m}}\leq{\mathfrak{n}}$, to ${\mathfrak{m}}={\mathfrak{n}}$.

Dowód. (1) Niech $A$ będzie zbiorem mocy ${\mathfrak{n}}$ zawierającym podzbiór $B$ mocy ${\mathfrak{m}}$. Niech $A'$ będzie innym zbiorem mocy ${\mathfrak{n}}$. Zbiory $A$ i $A'$ są równoliczne, zatem istnieje bijekcja $f:A\to A'$. Widzimy, że zbiór $B'=f[B]$ jest podzbiorem zbioru $A'$, mocy ${\mathfrak{m}}$.

(2) Załóżmy, że $C$ jest zbiorem mocy $\kappa$. Na mocy (1), $C$ zawiera pewien podzbiór $A$ mocy ${\mathfrak{n}}$, który z kolei zawiera pewien podzbiór $B$ mocy ${\mathfrak{m}}$. Zatem $B$ jest również podzbiorem $C$ mocy ${\mathfrak{m}}$.

(3) wynika z twierdzenia Cantora-Bernsteina. Niech $A$ będzie zbiorem mocy ${\mathfrak{n}}$. Wtedy $A$ zawiera podzbiór $B$ mocy ${\mathfrak{m}}$ (bo ${\mathfrak{m}}\leq{\mathfrak{n}}$). Z kolei $B$ zawiera podzbiór $C$ mocy ${\mathfrak{n}}$ (bo ${\mathfrak{n}}\leq{\mathfrak{m}}$). Dlatego $C\subseteq B\subseteq A$ i $C\sim A$. Z twierdzenia 11.3 dostajemy, że $A\sim B$, czyli ${\mathfrak{m}}={\mathfrak{n}}$. $\Box$

Uwagę 12.4(3) również nazywa się twierdzeniem Cantora-Bernsteina. Oczywisćie mamy $\aleph_0\leq{\mathfrak{c}}$. Z twierdzenia Cantora mamy, że $\aleph_0\neq{\mathfrak{c}}$ (bo zbiór $\mathbb{R}$ jest nieprzeliczalny). Dlatego $\aleph_0<{\mathfrak{c}}$. Ta ostra nierówność jest nieprzypadkowa. Uogólnimy ją poniżej. Zaczniemy od dość zaskakującej uwagi.

Uwaga 12.5   $2^{\aleph_0}={\mathfrak{c}}$, innymi słowy zbiór liczb rzeczywistych jest równoliczny ze zbiorem wszystkich podzbiorów $\mathbb{N}$.

Dowód. Na mocy uwagi 12.4(3) wystarczy pokazać, że $2^{\aleph_0}\leq{\mathfrak{c}}$ i $2^{\aleph_0}\geq{\mathfrak{c}}$.

$\leq$. Z definicji, $2^{\aleph_0}$ to moc zbioru $\{0,1\}^{\mathbb{N}}$ wszystkich ciągów zerojedynkowych. Każdemu takiemu ciągowi $(a_n)$ możemy przypisać liczbę o rozwinięciu dziesiętnym $0,a_0a_1a_2\dots$. W ten sposób określamy funkcję różnowartościową $f:\{0,1\}^{\mathbb{N}}\to\mathbb{R}$. Zatem zbiór $Rng(f)$ jest podzbiorem $\mathbb{R}$ mocy $2^{\aleph_0}$. Czyli $2^{\aleph_0}\leq{\mathfrak{c}}$.

$\geq$. Z rodziału 11 wiemy, że przedział $(0,1)$ ma moc continuum. Każdej liczbie $x\in(0,1)$ przypisujemy ciąg zerojedynkowy kolejnych cyfr w rozwinięciu $x$ przy podstawie $2$. W ten sposób określamy funkcję różnowartościową przekształcającą zbiór $(0,1)$ w $\{0,1\}^{\mathbb{N}}$. Stąd dostajemy $2^{\aleph_0}\geq{\mathfrak{c}}$. $\Box$

Twierdzenie 12.6 (Cantor)   ${\mathfrak{m}}<2^{{\mathfrak{m}}}$.

Dowód. Niech $X$ będzie zbiorem mocy ${\mathfrak{m}}$. Wtedy zbiór ${\cal P}(X)$ jest mocy $2^{{\mathfrak{m}}}$. Przyporządkowanie elementowi $x\in X$ zbioru $\{x\}$ określa funkcję różnowartościową $X\to{\cal P}(X)$. Jej obraz jest podzbiorem zbioru ${\cal P}(X)$ mocy ${\mathfrak{m}}$. To pokazuje, że ${\mathfrak{m}}\leq 2^{{\mathfrak{m}}}$. By dokończyć dowód, wystarczy więc pokazać, że ${\mathfrak{m}}\neq 2^{{\mathfrak{m}}}$.

Przypuśćmy nie wprost, że ${\mathfrak{m}}= 2^{{\mathfrak{m}}}$, to znaczy, że zbiory $X$ i ${\cal P}(X)$ są równoliczne. Niech $f:X\to{\cal P}(X)$ będzie bijekcją. By uzyskać sprzeczność, znajdziemy podzbiór $Y$ zbioru $X$ różny od $f(x)$ dla wszystkich $x\in X$. Zbiór $Y$ definiujemy wzorem

$$x\in Y\Leftrightarrow x\not\in f(x).$$

Widzimy, że istotnie dla każdego $x\in X$ mamy $Y\neq f(x)$, gdyż zbiory $Y$ i $f(x)$ nie mają tych samych elementów: ``różnią się'' na elemencie $x$. $\Box$

Uwaga 12.4 mówi, że $\leq$ jest częściowym porządkiem na klasie liczb kardynalnych. Można się zastanawiać, czy jest to porządek liniowy. Innymi słowy, czy dla wszystkich zbiorów $X,Y$ mamy $\vert X\vert\leq\vert Y\vert$ lub $\vert Y\vert\leq\vert X\vert$. By to udowodnić, jako dodatkowego założenia potrzebujemy tak zwanego aksjomatu wyboru (zwanego również pewnikiem wyboru), który jest mniej oczywisty od dotychczas rozważanych własności zbiorów.

Aksjomat Wyboru. Jeśli $\{A_t:t\in T\}$ jest indeksowaną rodziną zbiorów niepustych, to istnieje funkcja $f$ (zwana funkcją wyboru) o dziedzinie $T$, taka że dla wszystkich $t\in T, f(t)\in A_t$.

Aksjomat wyboru, choć pozornie naturalny, ma jednak zaskakujące konsekwencje. Przykładowo wynika z niego, że kulę można podzielić na 5 części i złożyć z nich dwie kule identyczne z wyjściową (paradoks Banacha-Tarskiego). Przyjmujemy jednak zazwyczaj ten aksjomat w teorii mnogości, gdyż bez niego trudno byłoby udowodnić wiele naturalnych matematycznych twierdzeń (jak np. równoważność definicji funkcji ciągłej wg Heinego i wg Cauchy'ego). Prostą konsekwencją aksjomatu wyboru jest następująca uwaga.

Uwaga 12.7   Jeśli $f:A\to B$ jest surjekcją, to $\vert A\vert\geq\vert B\vert$.

Dowód. Dla $b\in B$ definiujemy zbiór $A_b$ jako $f^{-1}[\{b\}]$. Widzimy więc, że indeksowana rodzina zbiorów $\{A_b:b\in B\}$ jest partycją zbioru $A$ na zbiory niepuste. Na mocy aksjomatu wyboru istnieje funkcja wyboru $g:B\to A$ taka, że dla każdego $b\in B$ mamy $g(b)\in A_b$. Skoro zbiory $A_b,b\in B$ są rozłączne, to funkcja $g$ jest różnowartościowa. Dlatego mamy
$B\sim g[B]\subseteq A$, czyli $\vert B\vert\leq\vert A\vert$. $\Box$

Zamiast aksjomatu wyboru często używa się tak zwanego lematu Kuratowskiego-Zorna, który jest jego konsekwencją.

Lemat 12.8 (Kuratowski-Zorn)   Załóżmy, że $\leq$ jest częściowym porządkiem na zbiorze $X$ o tej własności, że każdy łańcuch w $X$ jest ograniczony z góry. Wtedy w zbiorze $X$ istnieje element maksymalny.

Używając lematu Kuratowskiego-Zorna możemy teraz udowodnić, że $\leq$ jest liniowym porządkiem na klasie liczb kardynalnych, tzn. że w stosunku do lematu 14.4 dodatkowo jest spójny.

Twierdzenie 12.9   ${\mathfrak{m}}\leq{\mathfrak{n}}$ lub ${\mathfrak{n}}\leq{\mathfrak{m}}$.

Dowód. Niech $X$ będzie zbiorem mocy ${\mathfrak{m}}$, zaś $Y$ zbiorem mocy ${\mathfrak{n}}$. Niech

$T=\{f:f$ jest bijekcją między pewnym podzbiorem $X$ i pewnym podzbiorem $Y\}$.

Na zbiorze $T$ określamy relację $\leq$ wzorem

$$f\leq g\Leftrightarrow g\mbox{ jest rozszerzeniem }f.$$

Widzimy, że $\leq$ jest częściowym porządkiem na zbiorze $T$. Ponadto spełnione są założenia lematu Kuratowskiego-Zorna.

Istotnie, jeśli $A\subseteq T$ jest łańcuchem, to możemy określić funkcję $g$ wzorem

$$g(x)=y\Leftrightarrow f(x)=y\mbox{ dla pewnego }f\in A.$$

Dziedzina funkcji $g$ jest sumą dziedzin wszystkich funkcji ze zbioru $A$, podobnie obraz $g$ jest sumą wszystkich obrazów funkcji z $A$. (Krócej moglibyśmy napisać, że $g=\bigcup A$.)

Widzimy, że $g\in T$ oraz $g$ jest ograniczeniem górnym łańcucha $A$.

Z lematu Kuratowskiego-Zorna dostajemy element maksymalny $f\in T$. Niech $X'=Dom(f)$ oraz $Y'=Rng(f)$. Wtedy $X'\sim Y'$. Twierdzimy, że

(a)

$X'=X$ lub $Y'=Y$.

Przypuśćmy, że nie. Wtedy istnieją elementy $a\in X\setminus X'$ i $b\in Y\setminus Y'$. Możemy określić wówczas funkcję $f':X'\cup\{a\}\to Y'\cup\{b\}$ rozszerzającą $f$, kładąc $f'(a)=b$. Wtedy $f'\in T, f'\geq f$ i $f'\neq f$, co przeczy maksymalności $f$.

Zgodnie z (a) mamy dwa przypadki. Gdy $X=X'$, to $X\sim Y'\subseteq Y$, czyli ${\mathfrak{m}}\leq{\mathfrak{n}}$. Gdy $Y=Y'$, to $Y\sim X'\subseteq X$, więc ${\mathfrak{n}}\leq{\mathfrak{m}}$. $\Box$

Z aksjomatu wyboru wynika, że dodawanie i mnożenie nieskończonych liczb kardynalnych jest bardzo łatwe. Mianowicie, gdy ${\mathfrak{m}}$ lub ${\mathfrak{n}}$ jest nieskończone, to

$${\mathfrak{m}}+{\mathfrak{n}}={\mathfrak{m}}\cdot{\mathfrak{n}}=\max\{{\mathfrak{m}},{\mathfrak{n}}\}.$$

Można to udowodnić przez indukcję pozaskończoną, o której wspomnimy później.

Nawet przy założeniu pewnika wyboru wiele pytań na temat zbiorów pozostaje otwartych. Najsłynniejszym takim problemem jest hipoteza continuum.

Hipoteza Continuum. Każdy nieprzeliczalny podzbiór zbioru liczb rzeczywistych jest równoliczny z $\mathbb{R}$.

Hipoteza ta mówi, że między liczbami $\aleph_0$ i ${\mathfrak{c}}$ nie ma żadnej innej liczby kardynalnej. Wiadomo, że hipotezy continuum nie można rozstrzygnąć na gruncie teorii mnogości Zermelo-Fraenkla z aksjomatem wyboru.