4. Rachunek zbiorów

Na zbiorach możemy wykonywać różne działania. Załóżmy, że $A$ i $B$ są zbiorami.
1. Zbiór

$$A\cup B=\{x:x\in A\lor x\in B\}$$

nazywamy sumą (mnogościową) zbiorów $A$ i $B$. Znak sumy $\cup$ czytamy jako ``plus''.
2. Zbiór

$$A\cap B=\{x:x\in A\land x\in B\}$$

nazywamy przekrojem (iloczynem mnogościowym) zbiorów $A$ i $B$. Znak przekroju $\cap$ odczytujemy jako ``razy''.
3. Zbiór

$$A\setminus B=\{x:x\in A\land x\not\in B\}$$

nazywamy różnicą (mnogościową) zbiorów $A$ i $B$. Znak $\setminus$ odczytujemy jako ``minus''.

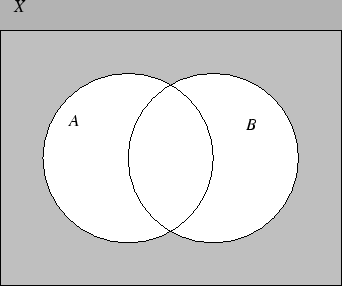
Zbiory opisane wyżej wygodnie jest przedstawiać na diagramach Venna.

Dla wszystkich $x$ zachodzą następujące równoważności.

$$x\in A\cup B\Leftrightarrow x\in A\lor x\in B$$

$$x\in A\cap B\Leftrightarrow x\in A\land x\in B$$

$$x\in A\setminus B\Leftrightarrow x\in A\land x\not\in B$$

W przypadku, gdy $A=\{x:W(x)\}$, zaś $B=\{x:V(x)\}$, dostajemy

$$A\cup B=\{x:W(x)\lor V(x)\},$$

$$A\cap B=\{x:W(x)\land V(x)\},$$

$$A\setminus B=\{x:W(x)\land\neg V(x)\}.$$

Działania na zbiorach odpowiadają w ten sposób operacjom logicznym na funkcjach zdaniowych.

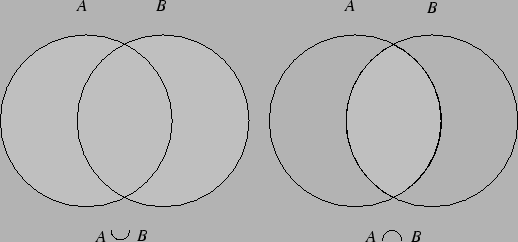
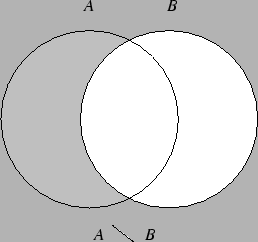
Przyjmujemy następującą definicję.

Definicja 4.1   Mówimy, że zbiory $A$ i $B$ są rozłączne, gdy nie mają wspólnych elementów. W tym przypadku ich przekrój jest zbiorem pustym $\emptyset$. Innymi słowy, zbiory $A$ i $B$ są rozłączne $\Leftrightarrow\ A\cap B=\emptyset$.

Przykład 1. Niech $A=\{0,1,2,3\}, B=\{2,3,4,5\}$. Dla każdego $x$ mamy:

$$x\in A\Leftrightarrow x=0\lor x=1\lor x=2\lor x=3,$$

$$x\in B\Leftrightarrow x=2\lor x=3\lor x=4\lor x=5.$$

Dlatego

$$x\in A\lor x\in B\Leftrightarrow x=0\lor x=1\lor x=2\lor x=3\lor x=4\lor x=5,$$

czyli $A\cup B=\{0,1,2,3,4,5\}$. Podobnie

$$x\in A\land x\in B\Leftrightarrow x=2\lor x=3$$

i

$$x\in A\land x\not\in B\Leftrightarrow x=0\lor x=1,$$

czyli

$$A\cap B=\{2,3\}\mbox{ i }A\setminus B=\{0,1\}.$$

Przykład 2. $A=\{a,b,c,d\}, B=\{c,d,e,f\}$. Zakładamy, że $a,b,c,d,e,f$ to różne przedmioty. Wtedy $A\cup B=\{a,b,c,d,e,f\},\ A\cap B=\{c,d\}, A\setminus B=\{a,b\}$.

Okazuje się, że własności działań $\cup$ i $\cap$ na zbiorach odpowiadają własnościom spójników logicznych $\lor$ i $\land$ wyrażonym w tautologiach na początku rozdziału 2 (tak więc zewnętrzne podobieństwo tych symboli jest nieprzypadkowe).

Własności $\cup$ i $\cap$.

1. $A\cup B=B\cup A, A\cap B=B\cap A$ (przemienność $\cup,\cap$).
2. $A\cup(B\cup C)=(A\cup B)\cup C, A\cap(B\cap C)=(A\cap B)\cap C$ (łączność $\cup,\cap$).
3. $A\cap(B\cup C)=(A\cap B)\cup(A\cap C)$ (rozdzielność $\cap$ względem $\cup$).
4. $A\cup(B\cap C)=(A\cup B)\cap(A\cup C)$ (rozdzielność $\cup$ względem $\cap$).
5. $A\cup A=A, A\cap A=A$.
6. $A\cup\emptyset=A, A\cap\emptyset=\emptyset$.

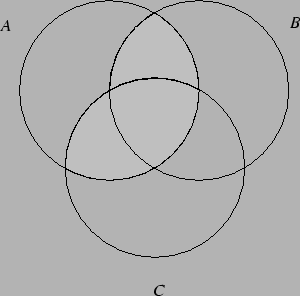
Przed przystąpieniem do dowodu tych równości (zwanych tożsamościami lub prawami rachunku zbiorów) warto unaocznić je sobie zaznaczając odpowiednie zbiory na diagramach Venna. Dla przykładu robimy to poniżej dla zbioru $A\cap(B\cup C)=(A\cap B)\cup(A\cap C)$. Ponadto, podobnie jak w przypadku $\lor$ i $\land$, na mocy łączności $\cap$ i $\cup$ możemy pomijać nawiasy w wielokrotnych przekrojach i sumach.

Dowód. (1) Dla dowodu równości $A\cup B=B\cup A$ wystarczy udowodnić, że dla wszystkich $x$ mamy:

$$x \in A \cup B\Leftrightarrow x \in B \cup A.$$

Weźmy więc dowolne $x$. Wtedy

$$x\in A\cup B$$

$$\Updownarrow$$

$$x\in A\lor x\in B$$

$$\Updownarrow$$

$$x\in B\lor x\in A$$

$$\Updownarrow$$

$$x\in B\cup A$$

W pierwszej i trzeciej równoważności korzystamy z definicji $\cup$, w drugiej równoważności korzystamy z tautologii $p\lor q\Leftrightarrow q\lor p$ (przemienność $\lor$).

Dlatego $x\in A\cup B\Leftrightarrow x\in B\cup A$, czyli $A\cup B=B\cup A$.

W dowodzie $A\cap B=B\cap A$ stosujemy definicję $\cap$ i tautologię $p\land q\Leftrightarrow q\land p$ (przemienność $\land$).

(2) W dowodzie stosujemy definicje $\cup,\cap$ i tautologie $p\lor(q\lor r)\Leftrightarrow(p\lor q)\lor r$ (łączność $\lor$) i $p\land(q\land r)\Leftrightarrow(p\land q)\land r$ (łączność $\land$). Przykładowo udowodnimy łączność $\cup$. W tym celu wystarczy pokazać, że dla dowolnego $x$ mamy

$$x\in A\cup(B\cup C)\Leftrightarrow x\in (A\cup B)\cup C.$$

Rozważmy więc dowolne $x$. Mamy następujący ciąg zdań równoważnych.

$$x\in A\cup(B\cup C)$$

$$\Updownarrow$$

$$x\in A\lor x\in (B\cup C)$$

$$\Updownarrow$$

$$x\in A\lor(x\in B\lor x\in C)$$

$$\Updownarrow$$

$$(x\in A\lor x\in B)\lor x\in C$$

$$\Updownarrow$$

$$(x\in A\cup B)\lor x\in C$$

$$\Updownarrow$$

$$x\in (A\cup B)\cup C$$

Dlatego $x\in A\cup(B\cup C)\Leftrightarrow x\in (A\cup B)\cup C$, czego chcieliśmy dowieść.

W dowodach dalszych punktów stosujemy odpowiednio tautologie
$p\land(q\lor r)\Leftrightarrow(p\land q)\lor(p\land r)$ (rozdzielność $\land$ względem $\lor$),
$p\lor(q\land r)\Leftrightarrow(p\lor q)\land(p\lor r)$ (rozdzielność $\lor$ względem $\land$),
$p\lor p\Leftrightarrow p, p\land p\Leftrightarrow p, p\lor 0\Leftrightarrow p, p\land 0\Leftrightarrow 0$. $\Box$

Inkluzja zbiorów. Mówimy, że zbiór $A$ jest podzbiorem zbioru $B$ wtedy i tylko wtedy, gdy każdy element zbioru $A$ jest elementem zbioru $B$. Fakt ten zapisujemy symbolicznie w postaci $A\subseteq B$. W tej sytuacji mówimy też, że zbiór $A$ zawiera się w zbiorze $B$ oraz że zbiór $B$ jest nadzbiorem zbioru $A$. Mamy więc

$$A\subseteq B\Leftrightarrow(\mbox{ dla każdego }x, x\in A\Rightarrow x\in B).$$

Powyższa równoważność może być również przyjęta za definicję pojęcia zawierania zbiorów. Zawieranie zbiorów nazywamy też inkluzją zbiorów.

Mówimy, że zbiór $A$ jest podzbiorem właściwym zbioru $B$ wtedy i tylko wtedy, gdy $A$ jest podzbiorem $B$ i $A$ jest różny od $B$. Symbolicznie fakt ten zapisujemy w postaci $A\subset B$. Mówimy wówczas, że $B$ jest nadzbiorem właściwym zbioru $A$. Mamy więc

$$A\subset B\Leftrightarrow A\subseteq B\land A\neq B.$$

Tu $A\neq B$ jest skrótem zdania $\neg(A=B)$.

Na przykład mamy ${\mathbb{N}}\subset{\mathbb{Z}}\subset{\mathbb{Q}}\subset{\mathbb{R}}$, jak również ${\mathbb{N}}\supset\{0,2,3,5\}\supset\{0,2\}$.

Wprost z definicji dostajemy, że $\emptyset$ i zbiór $A$ są podzbiorami zbioru $A$. $\emptyset$ nazywamy podzbiorem trywialnym zbioru $A$, zaś $A$ podzbiorem niewłaściwym zbioru $A$.

Należy tu położyć nacisk na poprawną terminologię: element $x$ zbioru $X$ należy do zbioru $X$, zaś podzbiór $Y$ zbioru $X$ zawiera się w zbiorze $X$. Może się zdarzyć, że zbiór $Y$ równocześnie zawiera się w zbiorze $X$ (tzn. jest jego podzbiorem), jak i należy do zbioru $X$ (tzn. jest jego elementem).

Przykład 1. Niech $X=\{\{\emptyset\}\}$ zaś $Y=\{\emptyset\}$. Oba zbiory $X$ i $Y$ są jednoelementowe. Jedynym elementem zbioru $X$ jest $\{\emptyset\}$, czyli zbiór $Y$. Dlatego $Y$ należy do $X$ (czyli $Y\in X$). Nie jest jednak prawdą, że zbiór $Y$ zawiera się w zbiorze $X$, nie jest on bowiem podzbiorem zbioru $X$. Mianowicie jedynym elementem zbioru $Y$ jest zbiór pusty $\emptyset$. I niestety ten właśnie element nie należy do zbioru $X$ (bo jedynym elementem zbioru $X$ jest właśnie zbiór $Y$ oraz $Y\neq\emptyset$).

Przykład 2. Niech $X=\{\emptyset,\{\emptyset\}\}$, zaś $Y=\{\emptyset\}$. Tu $Y$ należy do $X$ oraz zawiera się w $X$.

Poniżej podajemy własności inkluzji zbiorów i dalsze prawa rachunku zbiorów.

1. Jeśli $A\subseteq B$ i $B\subseteq A$, to $A=B$.

2. (przechodniość inkluzji) Jeśli $A\subseteq B$ i $B\subseteq C$, to $A\subseteq C$.

3. $A\cap B\subseteq A\subseteq A\cup B, A\setminus B\subseteq A$.

4. Jeśli $A\subseteq C$ i $B\subseteq D$, to $A\cup B\subseteq C\cup D$ i $A\cap B\subseteq C\cap D$.

5. $A\subseteq B\Leftrightarrow A\cup B=B, A\subseteq B\Leftrightarrow A\cap B=A$.

6. $A\cap B=A\setminus(A\setminus B)$.

7. $A\cup (B\setminus A)=A\cup B$.

8. $A\setminus(A\cap B)=A\setminus B$.

9. $A\cap(B\setminus C)=(A\cap B)\setminus C$.

Dowód. (1) Załóżmy, że $A\subseteq B$ i $A\supseteq B$. Znaczy to, że dla każdego $x$ mamy

$$x\in A\Rightarrow x\in B\mbox{ i }x\in A\Leftarrow x\in B,$$

czyli

$$x\in A\Leftrightarrow x\in B.$$

Zatem $A=B$.

(2) Załóżmy, że $A\subseteq B$ i $B\subseteq C$. Pokażemy, że $A\subseteq C$. Na mocy definicji inkluzji, $A\subseteq C$ oznacza, że dla wszystkich $X$, jeśli $x\in A$, to $x\in C$. Aby tego dowieść, rozważmy dowolne $x\in A$. Skoro $A\subseteq B$, to na mocy definicji $\subseteq$, $x\in B$. Skoro $B\subseteq C$, to na mocy definicji $\subseteq$, $x\in C$, czego należało dowieść.

W punkcie (3) udowodnimy, że $A\cap B\subseteq A$. W tym celu rozważmy dowolny element $x$ zbioru $A\cap B$. Na mocy definicji $\cap$, $x$ należy zarówno do $A$, jak i do $B$. W szczególności $x\in A$. W ten sposób pokazaliśmy, że dla dowolnego $x$ mamy

$$x\in A\cap B\Rightarrow x\in A,$$

czyli $A\cap B\subseteq A$.

Dowody pozostałych punktów pozostawiamy jako ćwiczenie. $\Box$

Przestrzeń, dopełnienie zbioru. Spójnikom logicznym $\land$ i $\lor$ odpowiadają działania $\cap$ i $\cup$ na zbiorach. Dotychczas nie wprowadziliśmy działania na zbiorach odpowiadającego spójnikowi negacji. Często zdarza się, że rozważamy podzbiory ustalonego zbioru $X$. W takiej sytuacji zbiór $X$ nazywamy przestrzenią. W tym kontekście negacji odpowiada tak zwane dopełnienie zbioru.

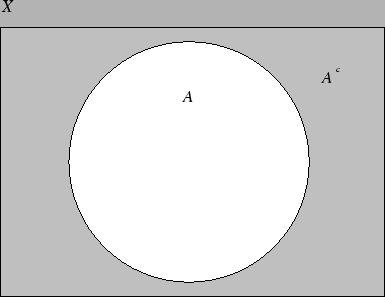
Dla zbioru $A\subseteq X$ zbiór $A^c=X\setminus A$ nazywamy dopełnieniem zbioru $A$ (w przestrzeni $X$). Zatem dla wszystkich $x\in X$ mamy

$$x\in A^c\Leftrightarrow x\not\in A.$$

W przypadku, gdy $A=\{x\in X: W(x)\}$, mamy $A^c=\{x\in X:\neg W(x)\}$. Dopełnienie zbioru zaznaczamy na diagramie Venna w następujący sposób.

Używając operacji dopełnienia zbioru możemy wyrazić kolejne prawa (tożsamości) rachunku zbiorów. Mianowicie, dla zbiorów $A,B\subseteq X$ mamy:

1. $X^c=\emptyset, \emptyset^c=X$.
2. $(A^c)^c=A$.
3. $A\cup A^c=X, A\cap A^c=\emptyset$.
4. $(A\cup B)^c=A^c\cap B^c,\ (A\cap B)^c=A^c\cup B^c$ (prawa de Morgana rachunku zbiorów).
5. $A\cap X=A, A\cup X=X$.

Przykładowo uzasadnimy część punktu 4. Korzystając z definicji oraz prawa de Morgana dla $\lor$, dla każdego $x\in X$ mamy ciąg zdań równoważnych:

$$x\in (A\cup B)^c$$

$$\Updownarrow$$

$$\neg(x\in A\cup B)$$

$$\Updownarrow$$

$$\neg(x\in A\lor x\in B)$$

$$\Updownarrow$$

$$(\neg x\in A)\land(\neg x\in B)$$

$$\Updownarrow$$

$$x\in A^c\land x\in B^c$$

$$\Updownarrow$$

$$x\in A^c\cap B^c.$$

Zatem dla wszystkich $x\in X$ mamy $x\in (A\cup B)^c\Leftrightarrow x\in A^c\cap B^c$. Oba zbiory $(A\cup B)^c$ i $A^c\cap B^c$ są podzbiorami przestrzeni $X$. Wynika więc stąd, że mają te same elementy i $(A\cup B)^c=A^c\cap B^c$. $\Box$

Warto unaocznić sobie powyższe prawa rachunku zbiorów na diagramach Venna dla podzbiorów przestrzeni $X$. Przykładowo zaznaczymy na diagramie Venna zbiór $(A\cup B)^c=A^c\cap B^c$.

Na koniec rozważań o rachunku zbiorów poznamy jeszcze operację różnicy symetrycznej i zbioru potęgowego. Różnicą symetryczną zbiorów $A$ i $B$ nazywamy zbiór

$$A\triangle B=(A\setminus B)\cup(B\setminus A).$$

Zbiorem potęgowym zbioru $A$ nazywamy zbiór

$${\cal P}(A)=\{B:B\subseteq A\},$$

czyli zbiór wszystkich podzbiorów zbioru $A$. Nazwę zbioru potęgowego uzasadnia następująca uwaga.

Uwaga 4.2   Jeśli $A$ jest skończonym zbiorem $n$-elementowym, to zbiór ${\cal P}(A)$ ma $2^n$ elementów (tzn. jest dokładnie $2^n$ różnych podzbiorów zbioru $A$).

Dowód. Dowód przeprowadzimy na przykładzie zbioru $4$-elementowego $A=\{a_1,a_2,a_3,a_4\}$. Na ile sposobów możemy wybrać podzbiór $B$ zbioru $A$ ? Podzbiór $B$ jest wyznaczony przez swoje elementy, które należą do $A$. Zatem mamy następujące możliwości:

1. $a_1$ może należeć do $B$ lub nie.

2. $a_2$ może należeć do $B$ lub nie.

3. $a_3$ może należeć do $B$ lub nie.

4. $a_4$ może należeć do $B$ lub nie.

W każdym z punktów 1-4 mamy $2$ możliwości, punkty 1.-4. są wzajemnie niezależne. Dlatego łącznie mamy $2\times 2\times 2\times 2=2^4$ możliwości, i tyleż różnych podzbiorów $B$ zbioru $A$. $\Box$

Jako ćwiczenie sugerujemy czytelnikowi wypisanie wszystkich podzbiorów zbioru $4$-elementowego $A=\{a_1,\dots,a_4\}$. Najlepsza metoda, to wypisywać kolejno podzbiory $0$-elementowe (jest tylko jeden: zbór pusty $\emptyset$), 1-elementowe, 2-elementowe, 3-elementowe i wreszcie 4-elementowe (jest tylko jeden: cały zbiór $A$). Wiadomo, że jest dokładnie ${n\choose k}$ $k$-elementowych podzbiorów zbioru $n$-elementowego.

W szczególności zbiór potęgowy zbioru pustego ${\cal P}(\emptyset)$ ma $2^0=1$ element ($\emptyset$ jest $0$-elementowy). Jedynym elementem zbioru ${\cal P}(\emptyset)$ jest zbiór pusty $\emptyset$, który jest tu zarówno podzbiorem trywialnym, jak i niewłaściwym.