Definicja 2..1
Mówimy, że formuły 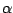 i
i 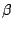 są równoważne,
gdy formuła
są równoważne,
gdy formuła
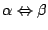 jest tautologią.
jest tautologią.
Uwaga 2..2
Formuły 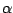 i
i 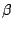 są równoważne wtedy i
tylko wtedy, gdy mają te same tabelki wartości logicznych.
są równoważne wtedy i
tylko wtedy, gdy mają te same tabelki wartości logicznych.
Następujące tautologie opisują własności spójników 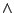 i
i
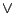 . Zwróćmy uwagę, że tautologie te mówią o równoważności
pewnych formuł zdaniowych.
. Zwróćmy uwagę, że tautologie te mówią o równoważności
pewnych formuł zdaniowych.
-
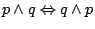 i
i
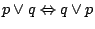 (przemienność
(przemienność 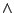 i
i 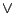 )
)
-
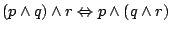 i
i
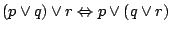 (łączność
(łączność 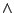 i
i
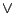 )
)
-
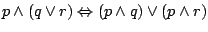 (rozdzielność
(rozdzielność 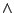 względem
względem 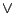 )
)
-
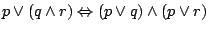 (rozdzielność
(rozdzielność 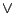 względem
względem 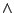 )
)
-
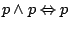 i
i
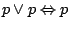
-
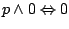 i
i
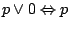
-
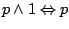 i
i
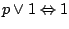
Zauważmy,
że gdy w wyliczonych wyżej tautologiach zastąpimy zmienne zdaniowe przez zmienne
liczbowe, symbol
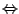 przez znak równości, zaś
spójniki
przez znak równości, zaś
spójniki 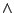 i
i 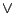 przez symbole mnożenia
przez symbole mnożenia  i dodawania
i dodawania
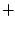 , to wówczas otrzymamy wyrażenia algebraiczne, które w wielu
przypadkach będą tożsamościami. Na przykład tautologie z punktu
2. odpowiadają w ten sposób prawom łączności mnożenia i
dodawania:
, to wówczas otrzymamy wyrażenia algebraiczne, które w wielu
przypadkach będą tożsamościami. Na przykład tautologie z punktu
2. odpowiadają w ten sposób prawom łączności mnożenia i
dodawania:
Dzięki łączności w wyrażeniach tego typu w algebrze możemy
opuszczać nawiasy. Podobnie w rachunku zdań możemy opuszczać
nawiasy w wielokrotnych koniunkcjach i alternatywach.
Dotychczas rozważaliśmy spójniki logiczne odpowiadające spójnikom
występującym w mowie potocznej. Możemy również definiować
abstrakcyjne spójniki logiczne poprzez zadanie tabelki wartości
logicznych.
Na przykład, by zdefiniować abstrakcyjny dwuargumentowy spójnik
logiczny 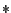 ,
wystarczy wypełnić tabelkę
,
wystarczy wypełnić tabelkę
zastępując znaki 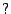 przez
przez 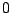 lub
lub 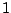 . Można to uczynić na
. Można to uczynić na
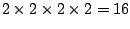 sposobów. Dlatego jest
sposobów. Dlatego jest 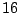 nierównoważnych dwuargumentowych spójników logicznych.
nierównoważnych dwuargumentowych spójników logicznych.
Podobnie określamy 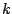 -argumentowe spójniki logiczne dla
-argumentowe spójniki logiczne dla
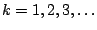 Przy pomocy
Przy pomocy 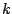 -argumentowego spójnika
-argumentowego spójnika 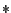 ze zdań
ze zdań
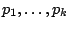 tworzymy nowe zdanie
tworzymy nowe zdanie
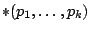 . Oczywiście
jest
. Oczywiście
jest 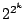 nierównoważnych
nierównoważnych 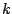 -argumentowych spójników
logicznych. Zazwyczaj rozważamy jednak spójniki jedno i
dwuargumentowe.
-argumentowych spójników
logicznych. Zazwyczaj rozważamy jednak spójniki jedno i
dwuargumentowe.
Definicja 2..3
Mówimy, że spójnik dwuargumentowy 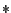 jest definiowalny przez formułę
jest definiowalny przez formułę
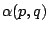 , gdy formuła
, gdy formuła 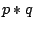 jest równoważna formule
jest równoważna formule
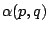 .
.
W przypadku, gdy spójnik 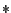 jest definiowalny przez formułę
jest definiowalny przez formułę
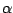 , w każdej formule
, w każdej formule 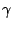 możemy zastąpić wystąpienia
spójnika
możemy zastąpić wystąpienia
spójnika 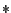 przez odpowiednie podstawienie formuły
przez odpowiednie podstawienie formuły 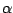 ,
otrzymując równoważną formułę
,
otrzymując równoważną formułę 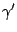 .
.
Przykłady. Z prawa de Morgana dla koniunkcji dostajemy, że
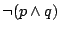 jest równoważne
jest równoważne
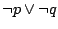 . Dlatego
. Dlatego
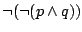 jest równoważne
jest równoważne
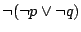 .
Na mocy prawa podwójnej negacji
.
Na mocy prawa podwójnej negacji
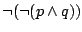 jest
równoważne formule
jest
równoważne formule 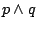 . Widzimy więc, że
. Widzimy więc, że
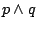 jest równoważne
jest równoważne
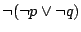 ,
,
tzn. formuła
jest tautologią.
Możemy więc powiedzieć, że spójnik koniunkcji 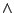 jest
definiowalny przy pomocy spójników negacji i alternatywy.
Używając spójników
jest
definiowalny przy pomocy spójników negacji i alternatywy.
Używając spójników 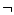 i
i 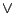 możemy w dowolnej
formule wyeliminować wystąpienia spójnika
możemy w dowolnej
formule wyeliminować wystąpienia spójnika 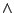 , dostając
formułę równoważną.
, dostając
formułę równoważną.
Podobnie dostajemy, że 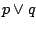 jest równoważne
jest równoważne
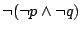 , czyli spójnik alternatywy jest definiowalny przy
pomocy
, czyli spójnik alternatywy jest definiowalny przy
pomocy 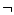 i
i 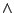 .
.
Korzystając z równoważności
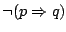 i
i 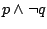 dostajemy, że formuła
dostajemy, że formuła
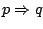 jest równoważna każdej
z formuł
jest równoważna każdej
z formuł
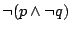 i
i 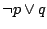 .
.
Uwaga 2..4
Każdy spójnik dwuargumentowy (ogólniej:
k-argumentowy) można zdefiniować przy pomocy negacji i dowolnego
spójnika spośród
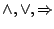 .
.
Wniosek 2..5
Każda formuła jest równoważna formule zbudowanej
przy pomocy 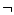 i dowolnego spójnika spośród
i dowolnego spójnika spośród
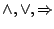 .
.
Przykład. Znajdziemy formułę równoważną formule
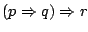 , zbudowaną przy pomocy
, zbudowaną przy pomocy 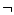 i
i
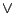 . W ciągu napisów poniżej znak
. W ciągu napisów poniżej znak 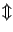 oznacza skrót:
``jest równoważne''. Korzystając z tego, że
oznacza skrót:
``jest równoważne''. Korzystając z tego, że
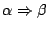 jest równoważne
jest równoważne
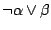 , mamy więc:
, mamy więc:
Dlatego formuła
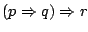 jest równoważna
formule
jest równoważna
formule
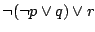 .
.
Definicja 2..6 (1)
Formuła 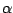 jest w postaci
alternatywno-koniunkcyjnej, gdy jest postaci
gdzie
jest w postaci
alternatywno-koniunkcyjnej, gdy jest postaci
gdzie 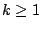 oraz dla
oraz dla 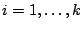 dla pewnego
dla pewnego 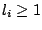 , gdzie każde
, gdzie każde 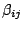 jest zmienną
zdaniową lub negacją zmiennej zdaniowej.
jest zmienną
zdaniową lub negacją zmiennej zdaniowej.
(2) Formuła 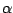 jest w postaci
koniunkcyjno-alternatywnej, gdy jest postaci
jest w postaci
koniunkcyjno-alternatywnej, gdy jest postaci
gdzie 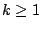 oraz dla
oraz dla 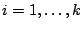 dla pewnego
dla pewnego 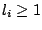 , gdzie każde
, gdzie każde 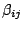 jest zmienną
zdaniową lub negacją zmiennej zdaniowej.
jest zmienną
zdaniową lub negacją zmiennej zdaniowej.
Na przykład formuła
jest postaci alternatywno-koniunkcyjnej, zaś formuła
jest postaci koniuncyjno-alternatywnej.
Uwaga 2..7 (1)
Każda formuła zdaniowa jest równoważna formule w postaci
alternatywno-koniunkcyjnej.
(2) Każda formuła zdaniowa jest równoważna formule w postaci
koniunkcyjno-alternatywnej.
Dowód. Dowód przeprowadzimy na przykładzie.
(1) Załóżmy, że tabelka wartości logicznych formuły
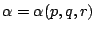 wygląda następująco:
wygląda następująco:
Z tabelki tej odczytujemy, że formuła 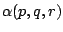 jest prawdziwa
wtedy i tylko wtedy, gdy
jest prawdziwa
wtedy i tylko wtedy, gdy
Zatem formuła 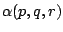 jest równoważna formule
jest równoważna formule
która jest w postaci alternatywno-koniunkcyjnej.
(2) Rozważmy formułę 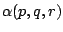 . Stosujemy punkt (1) do
formuły
. Stosujemy punkt (1) do
formuły
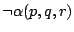 , znajdując równoważną jej
formułę w postaci alternatywno-koniunkcyjnej. Przypuśćmy dla
przykładu, że formuła
, znajdując równoważną jej
formułę w postaci alternatywno-koniunkcyjnej. Przypuśćmy dla
przykładu, że formuła
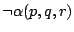 jest równoważna
formule
jest równoważna
formule
Wówczas wyjściowa formuła 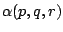 jest równoważna formule
jest równoważna formule
Stosując prawa de Morgana dla koniunkcji i alternatywy oraz
zastępując wyrażenia
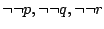 równoważnymi im wyrażeniami
równoważnymi im wyrażeniami 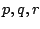 (prawo podwójnego przeczenia)
dostajemy:
(prawo podwójnego przeczenia)
dostajemy:
Ostatnia formuła jest już w postaci koniunkcyjno-alternatywnej. 
Rachunek zdań możemy stosować przy rozwiązywaniu równań i nierówności.
Przykład 1. Rozwiązać równanie
w
dziedzinie liczb rzeczywistych.
Niech 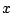 oznacza dowolną liczbę rzeczywistą. Wówczas równość
oznacza dowolną liczbę rzeczywistą. Wówczas równość
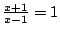 staje się zdaniem (prawdziwym lub nie) i dostajemy
następujący ciąg zdań równoważnych:
staje się zdaniem (prawdziwym lub nie) i dostajemy
następujący ciąg zdań równoważnych:
Ostatnie zdanie jest fałszywe dla każdej liczby 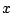 , zatem również
wyjściowe zdanie jest fałszywe dla każdej liczby
, zatem również
wyjściowe zdanie jest fałszywe dla każdej liczby 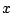 . Znaczy to, ze
równanie nie ma rozwiązań w liczbach rzeczywistych.
. Znaczy to, ze
równanie nie ma rozwiązań w liczbach rzeczywistych.
Przykład 2. Rozwiązać nierówność 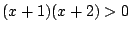 w
dziedzinie liczb rzeczywistych.
w
dziedzinie liczb rzeczywistych.
Niech 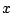 oznacza dowolną liczbę rzeczywistą. Wtedy korzystając z
własności działań na liczbach rzeczywistych dostajemy
następujący ciąg zdań równoważnych:
oznacza dowolną liczbę rzeczywistą. Wtedy korzystając z
własności działań na liczbach rzeczywistych dostajemy
następujący ciąg zdań równoważnych:
Skorzystaliśmy tu z faktu, że iloczyn dwóch liczb rzeczywistych jest
dodatni wtedy i tylko wtedy, gdy bądź obie są ujemne, bądź obie
są dodatnie.
Widzimy więc, że wyjściowa nierówność jest prawdziwa dokładnie
dla tych liczb rzeczywistych 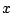 , które są większe od
, które są większe od 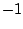 lub
mniejsze od
lub
mniejsze od 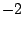 .
.
Przykład 3. Rozwiązać nierówność 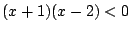 w
dziedzinie liczb rzeczywistych.
w
dziedzinie liczb rzeczywistych.
Niech 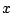 będzie dowolną liczbą rzeczywistą. Korzystając z faktu,
że iloczyn dwóch liczb rzeczywistych jest ujemny wtedy i tylko
wtedy, gdy jedna z nich jest dodatnia, a druga ujemna, mamy:
będzie dowolną liczbą rzeczywistą. Korzystając z faktu,
że iloczyn dwóch liczb rzeczywistych jest ujemny wtedy i tylko
wtedy, gdy jedna z nich jest dodatnia, a druga ujemna, mamy:
Jednak 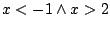 jest zdaniem fałszywym, więc korzystając z
tautologii
jest zdaniem fałszywym, więc korzystając z
tautologii
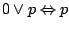 dostajemy, że powyższe zdanie
jest równoważne zdaniu
dostajemy, że powyższe zdanie
jest równoważne zdaniu 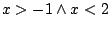 , co skrótowo zapisujemy jako
warunek
, co skrótowo zapisujemy jako
warunek 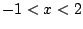 . Zatem liczby spełniające wyjściowe równanie to
dokładnie te liczby
. Zatem liczby spełniające wyjściowe równanie to
dokładnie te liczby 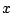 , dla których
, dla których 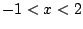 .
.
Przykład 4. Rozwiązać w dziedzinie liczb rzeczywistych
równanie
Sposób 1 (metoda przekształceń równoważnych). Niech 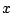 będzie
dowolną liczbą rzeczywistą. Korzystając z tego, że
będzie
dowolną liczbą rzeczywistą. Korzystając z tego, że 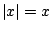 , gdy
, gdy
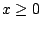 , oraz
, oraz 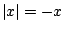 , gdy
, gdy 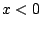 , wnioskujemy, że nasze równanie
jest równoważne następującej alternatywie:
, wnioskujemy, że nasze równanie
jest równoważne następującej alternatywie:
Pierwszy i trzeci człon tej alternatywy jest fałszywy dla dowolnego
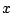 , dostajemy więc następujący ciąg zdań równoważnych:
, dostajemy więc następujący ciąg zdań równoważnych:
Metoda przekształceń równoważnych bywa kłopotliwa. Zamiast
niej można zastosować metodę implikacji, opisaną niżej.
Sposób 2 (metoda implikacji). W tej
metodzie w ciągu przekształcanych zdań niekiedy zdanie 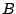 następujące po zdaniu
następujące po zdaniu 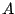 nie jest równoważne zdaniu
nie jest równoważne zdaniu 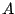 , lecz
jedynie z niego wynika, tzn. implikacja
, lecz
jedynie z niego wynika, tzn. implikacja
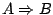 jest
prawdziwa. Fakt ten zapisujemy stosując skrót
jest
prawdziwa. Fakt ten zapisujemy stosując skrót 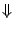 .
.
Niech więc 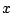 będzie dowolną liczbą rzeczywistą. Będziemy
korzystali z tego, że
będzie dowolną liczbą rzeczywistą. Będziemy
korzystali z tego, że
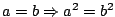 oraz że
oraz że 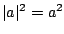 . Mamy
następujący ciąg zdań.
. Mamy
następujący ciąg zdań.
W tym ciągu przekształceń nie możemy zastąpić 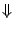 przez
przez
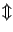 , gdyż implikacja odwrotna do
, gdyż implikacja odwrotna do
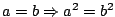 nie zawsze zachodzi. Powyższy ciąg przekształceń informuje nas
jednak, że jeśli
nie zawsze zachodzi. Powyższy ciąg przekształceń informuje nas
jednak, że jeśli 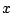 jest rozwiązaniem wyjściowego równania, to
jest rozwiązaniem wyjściowego równania, to
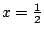 lub
lub
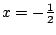 (na mocy przechodniości implikacji). Inaczej mówiąc, dla
wszystkich liczb rzeczywistych
(na mocy przechodniości implikacji). Inaczej mówiąc, dla
wszystkich liczb rzeczywistych 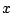 prawdziwa jest implikacja
prawdziwa jest implikacja
Znaczy to, że każde rozwiązanie 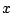 równania
równania
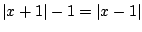 musi spełniać następnik tej implikacji,
tzn.
musi spełniać następnik tej implikacji,
tzn.
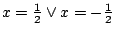 . Nie wynika stąd jeszcze, że
obie liczby
. Nie wynika stąd jeszcze, że
obie liczby
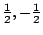 spełniają
wyjściowe równanie. Wymaga to sprawdzenia. W naszym przypadku liczba
spełniają
wyjściowe równanie. Wymaga to sprawdzenia. W naszym przypadku liczba
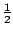 jest rozwiązaniem wyjściowego równania, zaś liczba
jest rozwiązaniem wyjściowego równania, zaś liczba
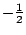 nie. Nie przeczy
to jednak prawdziwości implikacji
nie. Nie przeczy
to jednak prawdziwości implikacji 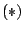 dla
dla
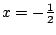 , gdyż wtedy jej
poprzednik jest fałszywy.
, gdyż wtedy jej
poprzednik jest fałszywy.
Ludomir Newelski
2006-08-29
![]() ,
wystarczy wypełnić tabelkę
,
wystarczy wypełnić tabelkę
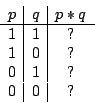
![]() -argumentowe spójniki logiczne dla
-argumentowe spójniki logiczne dla
![]() Przy pomocy
Przy pomocy ![]() -argumentowego spójnika
-argumentowego spójnika ![]() ze zdań
ze zdań
![]() tworzymy nowe zdanie
tworzymy nowe zdanie
![]() . Oczywiście
jest
. Oczywiście
jest ![]() nierównoważnych
nierównoważnych ![]() -argumentowych spójników
logicznych. Zazwyczaj rozważamy jednak spójniki jedno i
dwuargumentowe.
-argumentowych spójników
logicznych. Zazwyczaj rozważamy jednak spójniki jedno i
dwuargumentowe.
![]() jest równoważne
jest równoważne
![]() . Dlatego
. Dlatego
![]() jest równoważne
jest równoważne
![]() .
Na mocy prawa podwójnej negacji
.
Na mocy prawa podwójnej negacji
![]() jest
równoważne formule
jest
równoważne formule ![]() . Widzimy więc, że
. Widzimy więc, że
jest równoważne
,
![]() jest równoważne
jest równoważne
![]() , czyli spójnik alternatywy jest definiowalny przy
pomocy
, czyli spójnik alternatywy jest definiowalny przy
pomocy ![]() i
i ![]() .
.
![]() i
i ![]() dostajemy, że formuła
dostajemy, że formuła
![]() jest równoważna każdej
z formuł
jest równoważna każdej
z formuł
![]() i
i ![]() .
.
![]() , zbudowaną przy pomocy
, zbudowaną przy pomocy ![]() i
i
![]() . W ciągu napisów poniżej znak
. W ciągu napisów poniżej znak ![]() oznacza skrót:
``jest równoważne''. Korzystając z tego, że
oznacza skrót:
``jest równoważne''. Korzystając z tego, że
![]() jest równoważne
jest równoważne
![]() , mamy więc:
, mamy więc:
![]() jest w postaci
koniunkcyjno-alternatywnej, gdy jest postaci
jest w postaci
koniunkcyjno-alternatywnej, gdy jest postaci

![]() . Stosujemy punkt (1) do
formuły
. Stosujemy punkt (1) do
formuły
![]() , znajdując równoważną jej
formułę w postaci alternatywno-koniunkcyjnej. Przypuśćmy dla
przykładu, że formuła
, znajdując równoważną jej
formułę w postaci alternatywno-koniunkcyjnej. Przypuśćmy dla
przykładu, że formuła
![]() jest równoważna
formule
jest równoważna
formule
![]() jest równoważna formule
jest równoważna formule
![]() oznacza dowolną liczbę rzeczywistą. Wówczas równość
oznacza dowolną liczbę rzeczywistą. Wówczas równość
![]() staje się zdaniem (prawdziwym lub nie) i dostajemy
następujący ciąg zdań równoważnych:
staje się zdaniem (prawdziwym lub nie) i dostajemy
następujący ciąg zdań równoważnych:
![]() w
dziedzinie liczb rzeczywistych.
w
dziedzinie liczb rzeczywistych.
![]() oznacza dowolną liczbę rzeczywistą. Wtedy korzystając z
własności działań na liczbach rzeczywistych dostajemy
następujący ciąg zdań równoważnych:
oznacza dowolną liczbę rzeczywistą. Wtedy korzystając z
własności działań na liczbach rzeczywistych dostajemy
następujący ciąg zdań równoważnych:
![]() w
dziedzinie liczb rzeczywistych.
w
dziedzinie liczb rzeczywistych.
![]() będzie dowolną liczbą rzeczywistą. Korzystając z faktu,
że iloczyn dwóch liczb rzeczywistych jest ujemny wtedy i tylko
wtedy, gdy jedna z nich jest dodatnia, a druga ujemna, mamy:
będzie dowolną liczbą rzeczywistą. Korzystając z faktu,
że iloczyn dwóch liczb rzeczywistych jest ujemny wtedy i tylko
wtedy, gdy jedna z nich jest dodatnia, a druga ujemna, mamy:
![]() będzie
dowolną liczbą rzeczywistą. Korzystając z tego, że
będzie
dowolną liczbą rzeczywistą. Korzystając z tego, że ![]() , gdy
, gdy
![]() , oraz
, oraz ![]() , gdy
, gdy ![]() , wnioskujemy, że nasze równanie
jest równoważne następującej alternatywie:
, wnioskujemy, że nasze równanie
jest równoważne następującej alternatywie:
![]() następujące po zdaniu
następujące po zdaniu ![]() nie jest równoważne zdaniu
nie jest równoważne zdaniu ![]() , lecz
jedynie z niego wynika, tzn. implikacja
, lecz
jedynie z niego wynika, tzn. implikacja
![]() jest
prawdziwa. Fakt ten zapisujemy stosując skrót
jest
prawdziwa. Fakt ten zapisujemy stosując skrót ![]() .
.
![]() będzie dowolną liczbą rzeczywistą. Będziemy
korzystali z tego, że
będzie dowolną liczbą rzeczywistą. Będziemy
korzystali z tego, że
![]() oraz że
oraz że ![]() . Mamy
następujący ciąg zdań.
. Mamy
następujący ciąg zdań.