UNIVERSITY
OF WROCŁAW
 
Main Page
Contents
Online First
General Information
Instructions for authors


VOLUMES
43.1 42.2 42.1 41.2 41.1 40.2 40.1
39.2 39.1 38.2 38.1 37.2 37.1 36.2
36.1 35.2 35.1 34.2 34.1 33.2 33.1
32.2 32.1 31.2 31.1 30.2 30.1 29.2
29.1 28.2 28.1 27.2 27.1 26.2 26.1
25.2 25.1 24.2 24.1 23.2 23.1 22.2
22.1 21.2 21.1 20.2 20.1 19.2 19.1
18.2 18.1 17.2 17.1 16.2 16.1 15
14.2 14.1 13.2 13.1 12.2 12.1 11.2
11.1 10.2 10.1 9.2 9.1 8 7.2
7.1 6.2 6.1 5.2 5.1 4.2 4.1
3.2 3.1 2.2 2.1 1.2 1.1
 
 
WROCŁAW UNIVERSITY
OF SCIENCE AND
TECHNOLOGY

Contents of PMS, Vol. 26, Fasc. 2,
pages 261 - 281
 

CONVERGENCE RATE IN CLT FOR VECTOR-VALUED RANDOM FIELDS WITH SELF-NORMALIZATION

Alexander Bulinski
Natalya Kryzhanovskaya

Abstract: Statistical version of the central limit theorem (CLT) with random matrix normalization is established for random fields with values in a space 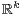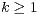Rk (k > 1 ). Dependence structure of the field under consideration is described in terms of the covariance inequalities for the class of bounded Lipschitz ”test functions” defined on finite disjoint collections of random vectors constituting the field. The main result provides an estimate of the convergence rate, over a family of convex bounded sets, in the CLT with random normalization.

2000 AMS Mathematics Subject Classification: 60F0S, 60F2S, 62E20, 62H20.

Key words and phrases: Random fields, dependence conditions, CLT, random matrix normalization, convergence rate.

Download:    Abstract    Full text   Abstract + References