Abstract: The main theme of Urbanik’s work was infinite divisibility and its ramifications. The aim of this memorial article is to trace the application of this theme in mathematical finance, one of the main growth areas in contemporary probability theory.

We begin in Section 1 with a discussion of the nature of prices. In particular, we focus on whether (or when) prices may be taken as continuous, with a view to using Lévy processes to model the case of prices with jumps. We turn in Section 2 to asset return distributions; prime candidates for modelling here include the normal, hyperbolic and Student 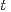cases. In Section 3, we turn to distributions of type 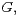in particular, those in which the mixing law is not only infinitely divisible but also self-decomposable (i.e. in the class 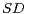), which includes all three cases above. Then in Section 4 we turn to the dynamic counterpart of this, in which the law of class 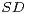occurs as the limit law of a stochastic process of Ornstein-Uhlenbeck type, with Lévy driving noise. Finally, in Section 5 we discuss stochastic volatility models.

2000 AMS Mathematics Subject Classification: Primary: 60E07, 60G51; Secondary: 91B28.

Key words and phrases: Infinite divisibility, self-decomposability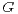, type , elliptically contoured distributions, mathematical finance, portfolios, stochastic volatility, processes of Ornstein-Uhlenbeck type.