ON BESOV REGULARITY OF BROWNIAN MOTIONS IN INFINITE
DIMENSIONS
Tuomas P. Hytönen
Mark C. Veraar
Abstract: We extend to the vector-valued situation some earlier work of Ciesielski and Roynette
on the Besov regularity of the paths of the classical Brownian motion. We also consider
a Brownian motion as a Besov space valued random variable. It turns out that a
Brownian motion, in this interpretation, is a Gaussian random variable with some
pathological properties. We prove estimates for the first moment of the Besov norm of
a Brownian motion. To obtain such results we estimate expressions of the form
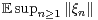 , where
, where
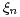 are
independent centered Gaussian random variables with values in a Banach space. Using isoperimetric
inequalities we obtain two-sided inequalities in terms of the first moments and the weak variances
of
are
independent centered Gaussian random variables with values in a Banach space. Using isoperimetric
inequalities we obtain two-sided inequalities in terms of the first moments and the weak variances
of 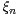 .
.
2000 AMS Mathematics Subject Classification: Primary: 60J65; Secondary: 28C20,
46E40, 60G17.
Key words and phrases: Gaussian random variable, maximal estimates, Besov-Orlicz
norm, non-separable Banach space, sample path.