UNIVERSITY
OF WROCŁAW
 
Main Page
Contents
Online First
General Information
Instructions for authors


VOLUMES
43.2 43.1 42.2 42.1 41.2 41.1 40.2
40.1 39.2 39.1 38.2 38.1 37.2 37.1
36.2 36.1 35.2 35.1 34.2 34.1 33.2
33.1 32.2 32.1 31.2 31.1 30.2 30.1
29.2 29.1 28.2 28.1 27.2 27.1 26.2
26.1 25.2 25.1 24.2 24.1 23.2 23.1
22.2 22.1 21.2 21.1 20.2 20.1 19.2
19.1 18.2 18.1 17.2 17.1 16.2 16.1
15 14.2 14.1 13.2 13.1 12.2 12.1
11.2 11.1 10.2 10.1 9.2 9.1 8
7.2 7.1 6.2 6.1 5.2 5.1 4.2
4.1 3.2 3.1 2.2 2.1 1.2 1.1
 
 
WROCŁAW UNIVERSITY
OF SCIENCE AND
TECHNOLOGY

Contents of PMS, Vol. 33, Fasc. 2,
pages 287 - 299
 

CONSTRUCTION OF A COMPACT QUANTUM GROUP FOR TRANSPOSITION-COLORING FUNCTION

Anna Kula

Abstract: We apply the Woronowicz construction of compact quantum group to the function which associates different parameters (colors) with transpositions generating the set of four-element permutation. We show that in the case when one of the parameters equals one, we get a non-trivial (non-commutative) compact quantum group which is a twisted product of 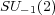SU (2) -1 and the two-dimensional torus.

2000 AMS Mathematics Subject Classification: Primary: 81R50; Secondary: 20G42.

Keywords and phrases: Quantum groups, twisted determinant condition, twisted product.

Download:    Abstract    Full text   Abstract + References