UNIVERSITY
OF WROCŁAW
 
Main Page
Contents
Online First
General Information
Instructions for authors


VOLUMES
43.2 43.1 42.2 42.1 41.2 41.1 40.2
40.1 39.2 39.1 38.2 38.1 37.2 37.1
36.2 36.1 35.2 35.1 34.2 34.1 33.2
33.1 32.2 32.1 31.2 31.1 30.2 30.1
29.2 29.1 28.2 28.1 27.2 27.1 26.2
26.1 25.2 25.1 24.2 24.1 23.2 23.1
22.2 22.1 21.2 21.1 20.2 20.1 19.2
19.1 18.2 18.1 17.2 17.1 16.2 16.1
15 14.2 14.1 13.2 13.1 12.2 12.1
11.2 11.1 10.2 10.1 9.2 9.1 8
7.2 7.1 6.2 6.1 5.2 5.1 4.2
4.1 3.2 3.1 2.2 2.1 1.2 1.1
 
 
WROCŁAW UNIVERSITY
OF SCIENCE AND
TECHNOLOGY

Contents of PMS, Vol. 34, Fasc. 1,
pages 1 - 22
 

PERSISTENCE PROBABILITIES FOR A BRIDGE OF AN INTEGRATED SIMPLE RANDOM WALK

Frank Aurzada
Steffen Dereich
Mikhail Lifshits

Abstract: We prove that an integrated simple random walk, where random walk and integrated random walk are conditioned to return to zero, has asymptotic probability 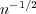n-1∕2 to stay positive. This question is motivated by random polymer models and proves a conjecture by Caravenna and Deuschel.

2000 AMS Mathematics Subject Classification: Primary: 60G50; Secondary: 60F99.

Keywords and phrases: Integrated random walk, local limit theorem, persistence probability.

Download:    Abstract    Full text   Abstract + References