ON PATHWISE STOCHASTIC INTEGRATION WITH RESPECT TO
SEMIMARTINGALES
Abstract: For any real-valued stochastic process 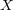 with cádlág paths we define non-empty
family of processes which have locally finite total variation, have jumps of the same order as
the process
with cádlág paths we define non-empty
family of processes which have locally finite total variation, have jumps of the same order as
the process 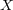 and uniformly approximate its paths on compacts. The application of the
defined class is the definition of stochastic integral with semimartingale integrand and
integrator as a limit of pathwise Lebesgue–Stieltjes integrals. This construction leads to the
stochastic integral with some correction term (different from the Stratonovich integral). Using
properties of a functional called truncated variation we compare the obtained result with
classical results of Wong–Zakai and Bichteler on pathwise stochastic integration.
and uniformly approximate its paths on compacts. The application of the
defined class is the definition of stochastic integral with semimartingale integrand and
integrator as a limit of pathwise Lebesgue–Stieltjes integrals. This construction leads to the
stochastic integral with some correction term (different from the Stratonovich integral). Using
properties of a functional called truncated variation we compare the obtained result with
classical results of Wong–Zakai and Bichteler on pathwise stochastic integration.
2000 AMS Mathematics Subject Classification: Primary: 60G46; Secondary:
60G17.
Keywords and phrases: Stochastic integral, truncated variation, double Skorokhod
map.