UNIVERSITY
OF WROCŁAW
 
Main Page
Contents
Online First
General Information
Instructions for authors


VOLUMES
43.2 43.1 42.2 42.1 41.2 41.1 40.2
40.1 39.2 39.1 38.2 38.1 37.2 37.1
36.2 36.1 35.2 35.1 34.2 34.1 33.2
33.1 32.2 32.1 31.2 31.1 30.2 30.1
29.2 29.1 28.2 28.1 27.2 27.1 26.2
26.1 25.2 25.1 24.2 24.1 23.2 23.1
22.2 22.1 21.2 21.1 20.2 20.1 19.2
19.1 18.2 18.1 17.2 17.1 16.2 16.1
15 14.2 14.1 13.2 13.1 12.2 12.1
11.2 11.1 10.2 10.1 9.2 9.1 8
7.2 7.1 6.2 6.1 5.2 5.1 4.2
4.1 3.2 3.1 2.2 2.1 1.2 1.1
 
 
WROCŁAW UNIVERSITY
OF SCIENCE AND
TECHNOLOGY

Contents of PMS, Vol. 34, Fasc. 1,
pages 97 - 117
 

DIMENSION RESULTS RELATED TO THE ST. PETERSBURG GAME

Peter Kern
Lina Wedrich

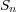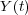Abstract: Let S n be the total gain in n repeated St. Petersburg games. It is known that n- 1(S - nlog n) n 2 converges in distribution along certain geometrically increasing subsequences and its possible limiting random variables can be parametrized as Y (t) with t ∈ [1,1] 2 . We determine the Hausdorff and box-counting dimension of the range and the graph for almost all sample paths of the stochastic process (Y (t)) t∈[1∕2,1] . The results are compared to the fractal dimension of the corresponding limiting objects when gains are given by a deterministic sequence initiated by Hugo Steinhaus.

2000 AMS Mathematics Subject Classification: Primary: 60G17; Secondary: 28A78, 28A80, 60G18, 60G22, 60G52.

Keywords and phrases: St. Petersburg game, semistable process, sample path, semi-selfsimilarity, range, graph, Hausdorff dimension, box-counting dimension, Steinhaus sequence, iterated function system, self-affine set.

Download:    Abstract    Full text   Abstract + References