Abstract: We prove that weak convergence of multivariate discrete Wiener integrals towards the continuous counterparts carries over to the application of discrete and continuous Wick calculus. This is done by the representation of arbitrary Wick products of Wiener integrals in terms of generalized Hermite polynomials and a discrete analog of the Hermite recursion. The result is a multivariate non-central limit theorem in the form of a Wick functional limit theorem. As an application we give approximations of multivariate processes based on fractional Brownian motions for arbitrary Hurst parameters .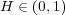

2000 AMS Mathematics Subject Classification: Primary: 60F05; Secondary: 60G15, 60H07.

Keywords and phrases: Wick calculus, discrete Wick calculus, weak convergence, central limit theorem.