UNIVERSITY
OF WROC£AW
 
Main Page
Contents
Online First
General Information
Instructions for authors


VOLUMES
43.1 42.2 42.1 41.2 41.1 40.2 40.1
39.2 39.1 38.2 38.1 37.2 37.1 36.2
36.1 35.2 35.1 34.2 34.1 33.2 33.1
32.2 32.1 31.2 31.1 30.2 30.1 29.2
29.1 28.2 28.1 27.2 27.1 26.2 26.1
25.2 25.1 24.2 24.1 23.2 23.1 22.2
22.1 21.2 21.1 20.2 20.1 19.2 19.1
18.2 18.1 17.2 17.1 16.2 16.1 15
14.2 14.1 13.2 13.1 12.2 12.1 11.2
11.1 10.2 10.1 9.2 9.1 8 7.2
7.1 6.2 6.1 5.2 5.1 4.2 4.1
3.2 3.1 2.2 2.1 1.2 1.1
 
 
WROC£AW UNIVERSITY
OF SCIENCE AND
TECHNOLOGY

Contents of PMS, Vol. 37, Fasc. 1,
pages 53 - 100
 

INTRINSIC COMPOUND KERNEL ESTIMATES FOR THE TRANSITION PROBABILITY DENSITY OF LÉVY-TYPE PROCESSES AND THEIR APPLICATIONS

Victoria Knopova
Aleksei Kulik

Abstract: Starting with an integro-differential operator 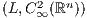(L,C2 (ℝn )) ∞ , we prove that its 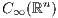C (ℝn ) ∞ -closure is the generator of a Feller process 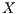X , which admits a transition probability density. To construct this transition probability density, we develop a version of the parametrix method and a verification procedure, which proves that the constructed object is the claimed one. As a part of the construction, we prove the intrinsic upper and lower estimates on the density. As an application of the constructed estimates we state the necessary and (separately) sufficient conditions under which a given Borel measure belongs to the Kato and Dynkin classes with respect to the constructed transition probability density.

2010 AMS Mathematics Subject Classification: Primary: 60J35; Secondary: 60J75, 35S05, 35S10, 47G30.

Keywords and phrases: Transition probability density, Lévy-type processes, pseudo-differential operator, generator, Levi’s parametrix method.

Download:    Abstract    Full text   Abstract + References