ON THE NUMBER OF REFLEXIVE AND SHARED NEAREST NEIGHBOR
PAIRS IN ONE-DIMENSIONAL UNIFORM DATA
Selim Bahadir
Elvan Ceyhan
Abstract: For a random sample of points in 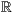 , we consider the number of pairs whose members
are nearest neighbors (NNs) to each other and the number of pairs sharing a common NN.
The pairs of the first type are called reflexive NNs, whereas the pairs of the latter type are
called shared NNs. In this article, we consider the case where the random sample of
size
, we consider the number of pairs whose members
are nearest neighbors (NNs) to each other and the number of pairs sharing a common NN.
The pairs of the first type are called reflexive NNs, whereas the pairs of the latter type are
called shared NNs. In this article, we consider the case where the random sample of
size 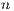 is from the uniform distribution on an interval. We denote the number of
reflexive NN pairs and the number of shared NN pairs in the sample by
is from the uniform distribution on an interval. We denote the number of
reflexive NN pairs and the number of shared NN pairs in the sample by 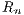 and
and 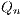 ,
respectively. We derive the exact forms of the expected value and the variance for both
,
respectively. We derive the exact forms of the expected value and the variance for both
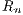 and
and 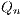 , and derive a recurrence relation for
, and derive a recurrence relation for 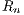 which may also be used to
compute the exact probability mass function (pmf) of
which may also be used to
compute the exact probability mass function (pmf) of 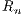 . Our approach is a novel
method for finding the pmf of
. Our approach is a novel
method for finding the pmf of 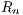 and agrees with the results in the literature. We
also present SLLN and CLT results for both
and agrees with the results in the literature. We
also present SLLN and CLT results for both 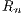 and
and 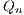 as
as 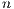 goes to infinity.
goes to infinity.
2010 AMS Mathematics Subject Classification: Primary: 05A05; Secondary: 05C20,
05C80, 60F05.
Keywords and phrases: Asymptotic normality, central limit theorem, exact
distribution, law of large numbers, nearest neighbor graphs and digraphs, random
permutation.