ON JOINT SUM/MAX STABILITY AND SUM/MAX DOMAINS OF
ATTRACTION
Katharina Hees
Hans-Peter Scheffler
Abstract: Let 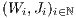 be a sequence of i.i.d.
be a sequence of i.i.d. 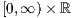 -valued random vectors.
Considering the partial sum of the first component and the corresponding maximum of the
second component, we are interested in the limit distributions that can be obtained under an
appropriate scaling. In the case that
-valued random vectors.
Considering the partial sum of the first component and the corresponding maximum of the
second component, we are interested in the limit distributions that can be obtained under an
appropriate scaling. In the case that 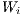 and
and 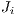 are independent, the joint distribution of the
sum and the maximum is the product measure of the limit distributions of the two
components. But if we allow dependence between the two components, this dependence can
still appear in the limit, and we need a new theory to describe the possible limit distributions.
This is achieved via harmonic analysis on semigroups, which can be utilized to
characterize the scaling limit distributions and describe their domains of attraction.
are independent, the joint distribution of the
sum and the maximum is the product measure of the limit distributions of the two
components. But if we allow dependence between the two components, this dependence can
still appear in the limit, and we need a new theory to describe the possible limit distributions.
This is achieved via harmonic analysis on semigroups, which can be utilized to
characterize the scaling limit distributions and describe their domains of attraction.
2010 AMS Mathematics Subject Classification: Primary: 60E07, 60F05; Secondary:
60E10.
Keywords and phrases: Sum stable, max stable, joint limit theorem.