UNIVERSITY
OF WROCŁAW
 
Main Page
Contents
Online First
General Information
Instructions for authors


VOLUMES
43.2 43.1 42.2 42.1 41.2 41.1 40.2
40.1 39.2 39.1 38.2 38.1 37.2 37.1
36.2 36.1 35.2 35.1 34.2 34.1 33.2
33.1 32.2 32.1 31.2 31.1 30.2 30.1
29.2 29.1 28.2 28.1 27.2 27.1 26.2
26.1 25.2 25.1 24.2 24.1 23.2 23.1
22.2 22.1 21.2 21.1 20.2 20.1 19.2
19.1 18.2 18.1 17.2 17.1 16.2 16.1
15 14.2 14.1 13.2 13.1 12.2 12.1
11.2 11.1 10.2 10.1 9.2 9.1 8
7.2 7.1 6.2 6.1 5.2 5.1 4.2
4.1 3.2 3.1 2.2 2.1 1.2 1.1
 
 
WROCŁAW UNIVERSITY
OF SCIENCE AND
TECHNOLOGY

Contents of PMS, Vol. 38, Fasc. 10,
pages 191 - 207
DOI: 10.19195/0208-4147.38.1.10
 

EXTREMES OF MULTIDIMENSIONAL STATIONARY GAUSSIAN RANDOM FIELDS

Natalia Soja-KukieŁa

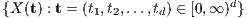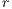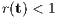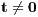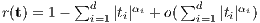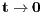Abstract: Let (X (t) : t = (t,t ,...,t) ∈ [0,∞ )d) 1 2 d be a centered stationary Gaussian field with almost surely continuous sample paths, unit variance and correlation function r satisfying r(t) < 1 for every t ⁄= 0 and ∑d αi ∑d αi r(t) = 1- i=1 |ti| + o( i=1|ti| ) , as t → 0 , with some α1,α2,...,αd ∈ (0,2] . 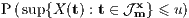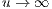The main result of this contribution is the description of the asymptotic behaviour of x P( sup(X (t) : t ∈ Jm ) ≤ u ) , as u → ∞ , for some Jordan-measurable sets 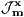x J m of volume proportional to d -1 P(sup(X (t) : t ∈ [0,1] ) > u) (1+ o(1)) .

2010 AMS Mathematics Subject Classification: Primary: 60G15; Secondary: 60G70, 60G60.

Keywords and phrases: Gaussian random field, supremum, limit theorem, asymptotics, Berman condition, strong dependence.

Download:    Abstract    Full text   Abstract + References