FRACTIONAL NEGATIVE BINOMIAL AND PÓLYA PROCESSES
Palaniappan Vellaisamy
Aditya Maheshwari
Abstract: In this paper, we define a fractional negative binomial process (FNBP) by replacing the
Poisson process by a fractional Poisson process (FPP) in the gamma subordinated form of the
negative binomial process. It is shown that the one-dimensional distributions of the FPP and
the FNBP are not infinitely divisible. Also, the space fractional Pólya process (SFPP) is
defined by replacing the rate parameter 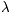 by a gamma random variable in the definition of
the space fractional Poisson process. The properties of the FNBP and the SFPP and the
connections to PDEs governing the density of the FNBP and the SFPP are also investigated.
by a gamma random variable in the definition of
the space fractional Poisson process. The properties of the FNBP and the SFPP and the
connections to PDEs governing the density of the FNBP and the SFPP are also investigated.
2010 AMS Mathematics Subject Classification: Primary: 60G22; Secondary:
60G51.
Keywords and phrases: Fractional negative binomial process, fractional Pólya process,
fractional Poisson process, infinite divisibility, Lévy process, PDEs.