ON A LIMIT STRUCTURE OF THE GALTON–WATSON BRANCHING
PROCESSES WITH REGULARLY VARYING GENERATING FUNCTIONS
Abstract: We investigate limit properties of discrete time branching processes with application of
the theory of regularly varying functions in the sense of Karamata. In the critical situation we
suppose that the offspring probability generating function has an infinite second
moment but its tail regularly varies. In the noncritical case, the finite moment of type
![E [xlnx]](files/39.1/HTML/39.1.4.abs0x.png) is required. The lemma on the asymptotic representation of the generating
function of the process and its differential analogue will underlie our conclusions.
is required. The lemma on the asymptotic representation of the generating
function of the process and its differential analogue will underlie our conclusions.
2000 AMS Mathematics Subject Classification: Primary: 60J80; Secondary:
60J85.
Keywords and phrases: Galton–Watson branching processes, regularly varying
functions, transition functions, invariant measures, limit theorems, 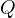 -processes.
-processes.