EMBEDDED MARKOV CHAIN APPROXIMATIONS IN SKOROKHOD
TOPOLOGIES
Abstract: We prove a 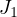 -tightness condition for embedded Markov chains and discuss four
Skorokhod topologies in a unified manner.
-tightness condition for embedded Markov chains and discuss four
Skorokhod topologies in a unified manner.
To approximate a continuous time stochastic process by discrete time Markov chains, one
has several options to embed the Markov chains into continuous time processes. On the one
hand, there is a Markov embedding which uses exponential waiting times. On the other
hand, each Skorokhod topology naturally suggests a certain embedding. These
are the step function embedding for 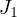 , the linear interpolation embedding for
, the linear interpolation embedding for
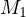 , the multistep embedding for
, the multistep embedding for 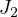 and a more general embedding for
and a more general embedding for 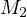 .
We show that the convergence of the step function embedding in
.
We show that the convergence of the step function embedding in 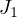 implies the
convergence of the other embeddings in the corresponding topologies. For the converse
statement, a
implies the
convergence of the other embeddings in the corresponding topologies. For the converse
statement, a 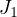 -tightness condition for embedded time-homogeneous Markov chains is
given.
-tightness condition for embedded time-homogeneous Markov chains is
given.
Additionally, it is shown that 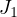 convergence is equivalent to the joint convergence in
convergence is equivalent to the joint convergence in
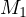 and
and 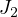 .
.
2000 AMS Mathematics Subject Classification: Primary: 60B10; Secondary: 60J75,
60J05.
Keywords and phrases: Markov chain embedding, tightness, Skorokhod space,
Skorokhod topologies, jump processes, Markov chain approximation.