ASYMPTOTIC BEHAVIOR FOR QUADRATIC VARIATIONS OF
NON-GAUSSIAN MULTIPARAMETER HERMITE RANDOM FIELDS
Abstract: Let ![(Zq,H ) d
t t∈[0,1]](files/39.2/HTML/39.2.8.abs0x.png) denote a
denote a 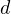 -parameter Hermite random field of order
-parameter Hermite random field of order 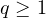 and
self-similarity parameter
and
self-similarity parameter 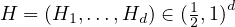 . This process is
. This process is 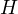 -self-similar, has
stationary increments and exhibits long-range dependence. Particular examples include
fractional Brownian motion (
-self-similar, has
stationary increments and exhibits long-range dependence. Particular examples include
fractional Brownian motion (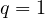 ,
, 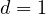 ), fractional Brownian sheet
), fractional Brownian sheet 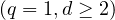 , the
Rosenblatt process (
, the
Rosenblatt process (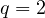 ,
, 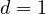 ) as well as the Rosenblatt sheet
) as well as the Rosenblatt sheet 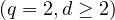 . For any
. For any
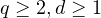 and
and 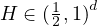 we show in this paper that a proper renormalization of
the quadratic variation of
we show in this paper that a proper renormalization of
the quadratic variation of 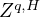 converges in
converges in 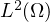 to a standard
to a standard 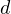 -parameter
Rosenblatt random variable with self-similarity index
-parameter
Rosenblatt random variable with self-similarity index 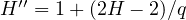 .
.
2000 AMS Mathematics Subject Classification: Primary: 60F05, 60H07; Secondary:
60G18, 60H05.
Keywords and phrases: Limit theorems, power variations, Hermite random field,
Rosenblatt random field, self-similar stochastic processes.