LIMIT THEOREMS FOR ARRAYS OF MAXIMAL ORDER STATISTICS
Abstract: Let 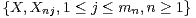 be independent and identically distributed
random variables with the Pareto distribution. Let
be independent and identically distributed
random variables with the Pareto distribution. Let 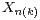 be the
be the 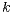 -th largest order statistic
from the
-th largest order statistic
from the 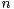 -th row of our array. This paper establishes unusual limit theorems involving
weighted sums for the sequence
-th row of our array. This paper establishes unusual limit theorems involving
weighted sums for the sequence 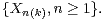
2000 AMS Mathematics Subject Classification: 60F0S, 60F1S.
Key words and phrases: Almost sure convergence; weak law of large numbers;
generalized law of the iterated logarithm.