UNIVERSITY
OF WROCŁAW
 
Main Page
Contents
Online First
General Information
Instructions for authors


VOLUMES
43.1 42.2 42.1 41.2 41.1 40.2 40.1
39.2 39.1 38.2 38.1 37.2 37.1 36.2
36.1 35.2 35.1 34.2 34.1 33.2 33.1
32.2 32.1 31.2 31.1 30.2 30.1 29.2
29.1 28.2 28.1 27.2 27.1 26.2 26.1
25.2 25.1 24.2 24.1 23.2 23.1 22.2
22.1 21.2 21.1 20.2 20.1 19.2 19.1
18.2 18.1 17.2 17.1 16.2 16.1 15
14.2 14.1 13.2 13.1 12.2 12.1 11.2
11.1 10.2 10.1 9.2 9.1 8 7.2
7.1 6.2 6.1 5.2 5.1 4.2 4.1
3.2 3.1 2.2 2.1 1.2 1.1
 
 
WROCŁAW UNIVERSITY
OF SCIENCE AND
TECHNOLOGY

Contents of PMS, Vol. 23, Fasc. 2,
pages 413 - 434
 

CENTRAL LIMIT THEOREM FOR A GAUSSIAN INCOMPRESSIBLE FLOW WITH ADDITIONAL BROWNIAN NOISE

Tomasz Miernowski

Abstract: We generalize the result of Komorowski and Papanicolaou published in [7]. We consider the solution of stochastic differential equation

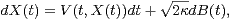
dX(t) = V(t,X(t))dt+ V~ 2kdB(t),
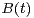
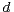
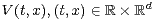
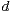
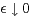
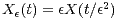
where B(t) is a standard d -dimensional Brownian motion and V(t,x),(t,x) (- R ŚRd , is a d -dimensional, incompressible, stationary, random Gaussian field decorrelating in finite time. We prove that the weak limit as e |, 0 of the family of rescaled processes Xe(t) = eX(t/e2) exists and may be identified as a certain Brownian motion.

2000 AMS Mathematics Subject Classification: 60F05 (60G15).

Key words and phrases: Weak convergence, random process, Gaussian field, incompressible flow, diffusion.

Download:    Abstract    Full text   Abstract + References