ADAPTIVE KERNEL ESTIMATION OF THE MODE IN A
NONPARAMETRIC RANDOM DESIGN REGRESSION MODEL
Abstract: In a nonparametric regression model with random design, where the regression
function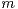 
is given by 
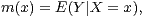estimation of the location 
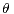(mode) and
size 
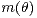of a unique maximum of 
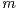is considered. As estimators, location 
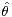and size
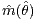of a maximum of the Nadaraya-Watson kernel estimator 
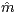for the curve 
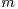are
chosen. Within this setting, we establish joint asymptotic normality and asymptotic
independence for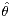 
and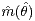 
(which can be exploited for constructing simultaneous
confidence intervals for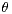 
and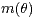 
) under mild local smoothness assumptions on 
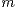and
the design density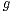 
(imposed in a neighborhood of 
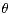). The bandwidths employed
for 
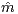are data-dependent and of plug-in type. This is handled by viewing the
estimators as stochastic processes indexed by a so-called scaling parameter and
proving functional central limit theorems for those processes. In the same way, we
obtain, as a by-product, an asymptotic normality result for the Nadaraya-Watson
estimator itself at a finite number of distinct points, which improves on previous results.
2000 AMS Mathematics Subject Classification: 62G05, 62G07.
Key words and phrases: Nonparametric regression, random design, mode, kernel
smoothing, Nadaraya-Watson estimator, weak convergence, functional central limit theorems.
