Abstract: We give a constructive proof of the fact that any Markov state (even non-homogeneous) on 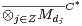is diagonalizable. However, due to the local entanglement effects, they are not necessarily of Ising type (Theorem 3.2). In addition, we prove that the underlying classical measure is Markov, and therefore, in the faithful case, it naturally defines a nearest neighbour Hamiltonian. In the translation invariant case, we prove that the spectrum of the two-point block of this Hamiltonian, in some cases, uniquely determines the type of the von Neumann factor generated by the Markov state (Theorem 5.3). In particular, we prove that, if all the quotients of the differences of two such eigenvalues are rational, then this factor is of type 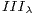for some 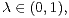and that, if this factor is of typ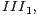e then these quotients cannot be all rational. We conjecture that the converses of these statements are also true.

2000 AMS Mathematics Subject Classification: 46L50, 82A15, 46L3S, 82B20, 60J99.

Key words and phrases: Quantum probability, mathematical statistical mechanics, classification of von Neumann factors, lattice systems, quantum Markov processes.