MARKOV PROCESSES CONDITIONED TO NEVER EXIT A SUBSPACE OF
THE STATE SPACE
Zbigniew Palmowski
Tomasz Rolski
Abstract: In this paper we study Markov processes never exiting (NE) a subspace 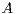 of
the state space
of
the state space 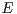 or, in other words, Markov processes conditioned to stay in
the subspace
or, in other words, Markov processes conditioned to stay in
the subspace 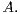 We show how the knowledge of the exact asymptotics of the
tail distribution of the exit time helps to find the suitable exponential martingale,
which, in turn, serves for the change of measure. Under the new probability measure
the process is the sought for never exiting one the subspace
We show how the knowledge of the exact asymptotics of the
tail distribution of the exit time helps to find the suitable exponential martingale,
which, in turn, serves for the change of measure. Under the new probability measure
the process is the sought for never exiting one the subspace 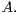 We also find its
extended generator and study relationships between the invariant measure (INE) and
the quasi-stationary (QS) distribution. We analyze in detail the PDMP processes.
We also find its
extended generator and study relationships between the invariant measure (INE) and
the quasi-stationary (QS) distribution. We analyze in detail the PDMP processes.
2000 AMS Mathematics Subject Classification: Primary: 60J25, 60J35.
Key words and phrases: Markov process, extended generator, exponential change of
measure, piecewise deterministic Markov process, workload conditioned to stay positive, NE
process, INE measure, quasi-stationary distribution.