THE FUNCTIONAL EQUATION AND STRICTLY SUBSTABLE RANDOM
VECTORS
Marta Borowiecka-Olszewska
Abstract: A random vector 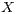 is
is 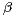 -substable,
-substable, ![b (- (0,2],](files/25.2/HTML/25.2.7.abs2x.png) if there exist a symmetric
if there exist a symmetric
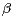 -stable random vector
-stable random vector 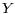 and a random variable
and a random variable 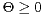 independent of
independent of  such that
such that
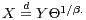 In this paper we investigate strictly
In this paper we investigate strictly 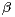 -substable random vectors which are
generated from a strictly
-substable random vectors which are
generated from a strictly 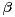 -stable random vector
-stable random vector 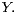 We study some of their properties. We
obtain the theorem that every strictly
We study some of their properties. We
obtain the theorem that every strictly 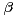 -stable random vector
-stable random vector 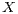 with
with 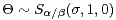 is
also strictly
is
also strictly 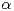 -stable,
-stable, 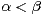 (for the case of random variable
(for the case of random variable 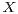 see, e.g., [1], [6]). The
opposite theorem is also satisfied, but we obtain something more. We obtain some
functional equation and we show that if a strictly
see, e.g., [1], [6]). The
opposite theorem is also satisfied, but we obtain something more. We obtain some
functional equation and we show that if a strictly 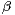 -substable random vector
-substable random vector 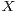 is
is 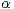 -stable, then it has to be strictly
-stable, then it has to be strictly 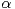 -stable and the mixing random variable
-stable and the mixing random variable
 has to have a distribution
has to have a distribution 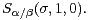 This is the main result of the paper.
This is the main result of the paper.
2000 AMS Mathematics Subject Classification: 60A10, 60E07, 60E10.
Key words and phrases: Stable, strictly stable, substable random vectors, spectral
measure, characteristic functions.