MONOTONICITY AND NON-MONOTONICITY OF DOMAINS OF
STOCHASTIC INTEGRAL OPERATORS
Abstract: A Lévy process on 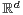 with distribution
with distribution 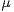 at time
at time 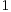 is denoted by
is denoted by
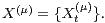 If the improper stochastic integral
If the improper stochastic integral 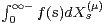 of
of 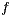 with respect to
with respect to
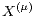 is definable, its distribution is denoted by
is definable, its distribution is denoted by 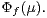 The class of all infinitely
divisible distributions
The class of all infinitely
divisible distributions 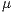 on
on 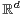 such that
such that 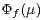 is definable is denoted by
is definable is denoted by 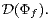 The class
The class 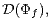 its two extensions
its two extensions 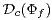 and
and 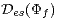 (compensated and
essential), and its restriction
(compensated and
essential), and its restriction 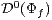 (absolutely definable) are studied. It is shown that
(absolutely definable) are studied. It is shown that
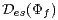 is monotonic with respect to
is monotonic with respect to 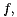 which means that
which means that 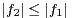 implies
implies
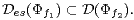 Further,
Further, 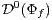 is monotonic with respect to
is monotonic with respect to 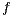 but neither
but neither
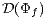 nor
nor 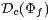 is monotonic with respect to
is monotonic with respect to 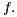 Furthermore, there exist
Furthermore, there exist 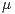 ,
, 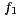 and
and 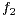 such that
such that 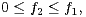
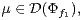 and
and 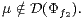 An explicit
example for this is related to some properties of a class of martingale Lévy processes.
An explicit
example for this is related to some properties of a class of martingale Lévy processes.
2000 AMS Mathematics Subject Classification: 60E07, 60G51, 60H05.
Key words and phrases: Improper stochastic integral, infinitely divisible distribution,
Lévy process, martingale Lévy process, monotonic.