CURSE OF DIMENSIONALITY IN APPROXIMATION OF RANDOM
FIELDS
M. A. Lifshits
E. V. Tulyakova
Abstract: Consider a random field of tensor product-type 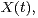
![t (- [0,1]d,](files/26.1/HTML/26.1.6.abs1x.png) given
by
given
by
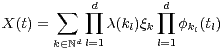
where
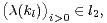
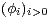
is an orthonormal system in
![L2[0,1]](files/26.1/HTML/26.1.6.abs5x.png)
and
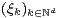
are
non-correlated random variables with zero mean and unit variance. We investigate the quality
of approximation (both in the average and in the probabilistic sense) to
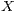
by the
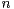
-term
partial sums
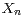
minimizing the quadratic error
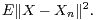
In the first part of the paper
we consider the case of fixed dimension
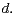
In the second part, following the suggestion of H.
Woźniakowski, we consider the same problem for
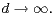
We show that, for any fixed
level of relative error, approximation complexity increases exponentially and we
find the explosion coefficient. We also show that the behavior of the probabilistic
and average complexity is essentially the same in the large domain of parameters.
2000 AMS Mathematics Subject Classification: 41A63, 60G1S.
Key words and phrases: Random fields, Gaussian processes, fractional Brownian sheet,
linear approximation error, complexity.