FINE STRUCTURE OF THE COMPLEX HYPERBOLIC BROWNIAN
MOTION AND RUDIN’S QUESTION
Abstract: We investigate the fine structure of the complex hyperbolic Brownian motion in
the unit ball of 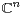 . It turns out that the generator of the process is locally very
close to the generator of some simple transformation of the classical Brownian
motion. This fact helps us to give an intuitive explanation why the invariant Laplace
operator in the unit ball of
. It turns out that the generator of the process is locally very
close to the generator of some simple transformation of the classical Brownian
motion. This fact helps us to give an intuitive explanation why the invariant Laplace
operator in the unit ball of 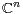 is a difference of two ordinary Laplace operators - the
question set by W. Rudin in his monograph Function Theory in the Unit Ball of
is a difference of two ordinary Laplace operators - the
question set by W. Rudin in his monograph Function Theory in the Unit Ball of
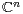 .
.
In the second part of the paper we find stochastic differential equations for the complex
hyperbolic Brownian motion on the ball model of the complex hyperbolic space
and furnish in this way an important tool in a further investigation of this process.
2000 AMS Mathematics Subject Classification: Primary: 32A07, 58J65; Secondary:
32Q35, 60H10, 60J65.
Keywords and phrases: Complex hyperbolic space, complex hyperbolic Brownian
motion, invariant Laplace operator.