Abstract: In infinite-dimensional Banach spaces there is no complete characterization of the Lévy exponents of infinitely divisible probability measures. Here we propose a calculus on Lévy exponents that is derived from some random integrals. As a consequence we prove that each selfdecomposable measure can by factorized as another selfdecomposable measure and its background driving measure that is s-selfdecomposable. This complements a result from the paper of Iksanov, Jurek and Schreiber in the Annals of Probability (2004).

2000 AMS Mathematics Subject Classification: Primary: 60E07, 60B12; Secondary: 60G51, 60H05.

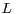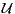Keywords and phrases: Banach space; selfdecomposable; class ; multiply selfdecomposable; s-selfdecomposable; class ; stable; infinitely divisible; Lévy-Khintchine formula; Lévy exponent; Lévy process; random integral.