A LIMIT THEOREM FOR SUMS OF BOUNDED FUNCTIONALS OF
LINEAR PROCESSES WITHOUT FINITE MEAN
Abstract: We consider the partial sum process of a bounded functional of a linear process and the
linear process has no finite mean. We assume the innovations of the linear process are
independent and identically distributed and that the distribution of the innovations belongs to
the domain of attraction of an 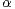 -stable law and satisfies some additional assumptions. Then
we establish the finite-dimensional convergence in distribution of the partial sum process to a
stable Lévy motion.
-stable law and satisfies some additional assumptions. Then
we establish the finite-dimensional convergence in distribution of the partial sum process to a
stable Lévy motion.
2000 AMS Mathematics Subject Classification: Primary: 60F5; Secondary:
60G51.
Keywords and phrases: Linear process, martingale, stable law, stable L é vy
motion.