UPPER AND LOWER CLASS SEPARATING SEQUENCES FOR BROWNIAN
MOTION WITH RANDOM ARGUMENT
Christoph Aistleitner
Siegfried Hörmann
Abstract: Let 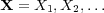 be a sequence of random variables, let
be a sequence of random variables, let
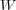 be a Brownian motion independent of
be a Brownian motion independent of 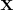 and let
and let 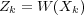 .
A numerical sequence
.
A numerical sequence 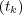 will be called an upper (lower) class sequence for
will be called an upper (lower) class sequence for 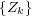 if
if
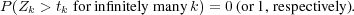
At a
first look one might be tempted to believe that a “separating line”
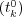
, say, between the
upper and lower class sequences for
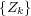
is directly related to the corresponding
counterpart
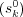
for the process
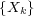
. For example, by using the law of the iterated
logarithm for the Wiener process a functional relationship
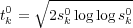 | (0.1) |
seems to be natural. If 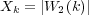 for a second Brownian motion
for a second Brownian motion 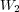 then we are
dealing with an iterated Brownian motion, and it is known that the multiplicative
constant
then we are
dealing with an iterated Brownian motion, and it is known that the multiplicative
constant 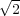 in (0.1) needs to be replaced by
in (0.1) needs to be replaced by 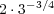 , contradicting this simple
argument.
, contradicting this simple
argument.
We will study this phenomenon from a different angle by letting 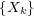 be an
i.i.d. sequence. It turns out that the relationship between the separating sequences
be an
i.i.d. sequence. It turns out that the relationship between the separating sequences 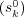 and
and
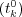 in the above sense depends in an interesting way on the extreme value behavior of
in the above sense depends in an interesting way on the extreme value behavior of
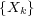 .
.
2000 AMS Mathematics Subject Classification: Primary: 60F15; Secondary: 60J65,
60G70.
Keywords and phrases: Brownian motion, extreme values, iterated Brownian motion,
upper-lower class test.