UNIVERSITY
OF WROCŁAW
 
Main Page
Contents
Online First
General Information
Instructions for authors


VOLUMES
43.1 42.2 42.1 41.2 41.1 40.2 40.1
39.2 39.1 38.2 38.1 37.2 37.1 36.2
36.1 35.2 35.1 34.2 34.1 33.2 33.1
32.2 32.1 31.2 31.1 30.2 30.1 29.2
29.1 28.2 28.1 27.2 27.1 26.2 26.1
25.2 25.1 24.2 24.1 23.2 23.1 22.2
22.1 21.2 21.1 20.2 20.1 19.2 19.1
18.2 18.1 17.2 17.1 16.2 16.1 15
14.2 14.1 13.2 13.1 12.2 12.1 11.2
11.1 10.2 10.1 9.2 9.1 8 7.2
7.1 6.2 6.1 5.2 5.1 4.2 4.1
3.2 3.1 2.2 2.1 1.2 1.1
 
 
WROCŁAW UNIVERSITY
OF SCIENCE AND
TECHNOLOGY

Contents of PMS, Vol. 31, Fasc. 2,
pages 227 - 238
 

WEAK-TYPE INEQUALITY FOR THE MARTINGALE SQUARE FUNCTION AND A RELATED CHARACTERIZATION OF HILBERT SPACES

Adam Osękowski

Abstract: Let 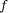f be a martingale taking values in a Banach space 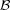B and let 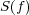S(f) be its square function. We show that if B is a Hilbert space, then

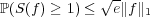
ℙ(S(f) ≥ 1) ≤ √e∥f∥ 1
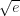
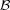
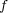
and the constant √- e is the best possible. This extends the result of Cox, who established this bound in the real case. Next, we show that this inequality characterizes Hilbert spaces in the following sense: if B is not a Hilbert space, then there is a martingale f for which the above weak-type estimate does not hold.

2000 AMS Mathematics Subject Classification: Primary: 60G42; Secondary: 46C15.

Keywords and phrases: Martingale, square function, weak type inequality, Banach space, Hilbert space.

Download:    Abstract    Full text   Abstract + References