UNIVERSITY
OF WROCŁAW
 
Main Page
Contents
Online First
General Information
Instructions for authors


VOLUMES
43.1 42.2 42.1 41.2 41.1 40.2 40.1
39.2 39.1 38.2 38.1 37.2 37.1 36.2
36.1 35.2 35.1 34.2 34.1 33.2 33.1
32.2 32.1 31.2 31.1 30.2 30.1 29.2
29.1 28.2 28.1 27.2 27.1 26.2 26.1
25.2 25.1 24.2 24.1 23.2 23.1 22.2
22.1 21.2 21.1 20.2 20.1 19.2 19.1
18.2 18.1 17.2 17.1 16.2 16.1 15
14.2 14.1 13.2 13.1 12.2 12.1 11.2
11.1 10.2 10.1 9.2 9.1 8 7.2
7.1 6.2 6.1 5.2 5.1 4.2 4.1
3.2 3.1 2.2 2.1 1.2 1.1
 
 
WROCŁAW UNIVERSITY
OF SCIENCE AND
TECHNOLOGY

Contents of PMS, Vol. 31, Fasc. 2,
pages 313 - 329
 

EIGENVALUE DISTRIBUTION OF LARGE SAMPLE COVARIANCE MATRICES OF LINEAR PROCESSES

Oliver Pfaffel
Eckhard Schlemm

Abstract: We derive the distribution of the eigenvalues of a large sample covariance matrix when the data is dependent in time. More precisely, the dependence for each variable 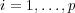i = 1,...,p is modelled as a linear process 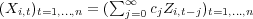(X ) = (∑ ∞ cZ ) i,t t=1,...,n j=0 j i,t-j t=1,...,n , where 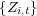(Z ) i,t are assumed to be independent random variables with finite fourth moments. 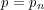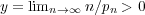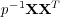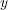If the sample size n and the number of variables p = p n both converge to infinity such that y = lim n∕p > 0 n→ ∞ n , then the empirical spectral distribution of p-1XXT converges to a non-random distribution which only depends on y and the spectral density of 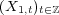(X ) 1,tt∈ℤ . In particular, our results apply to (fractionally integrated) ARMA processes, which will be illustrated by some examples.

2000 AMS Mathematics Subject Classification: Primary: 15A52; Secondary: 62M10.

Keywords and phrases: Eigenvalue distribution, fractionally integrated ARMA process, limiting spectral distribution, linear process, random matrix theory, sample covariance matrix.

Download:    Abstract    Full text   Abstract + References