UNIVERSITY
OF WROC£AW
 
Main Page
Contents
Online First
General Information
Instructions for authors


VOLUMES
43.2 43.1 42.2 42.1 41.2 41.1 40.2
40.1 39.2 39.1 38.2 38.1 37.2 37.1
36.2 36.1 35.2 35.1 34.2 34.1 33.2
33.1 32.2 32.1 31.2 31.1 30.2 30.1
29.2 29.1 28.2 28.1 27.2 27.1 26.2
26.1 25.2 25.1 24.2 24.1 23.2 23.1
22.2 22.1 21.2 21.1 20.2 20.1 19.2
19.1 18.2 18.1 17.2 17.1 16.2 16.1
15 14.2 14.1 13.2 13.1 12.2 12.1
11.2 11.1 10.2 10.1 9.2 9.1 8
7.2 7.1 6.2 6.1 5.2 5.1 4.2
4.1 3.2 3.1 2.2 2.1 1.2 1.1
 
 
WROC£AW UNIVERSITY
OF SCIENCE AND
TECHNOLOGY

Contents of PMS, Vol. 33, Fasc. 2,
pages 191 - 199
 

SOME DECOMPOSITIONS OF MATRIX VARIANCES

Zoltán Léka
Dénes Petz

Abstract: When 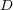D is a density matrix and 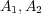A ,A 1 2 are self-adjoint operators, then the standard variance is a 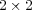2 ×2 matrix:

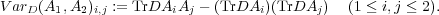
V arD(A1,A2)i,j := TrDAiAj - (TrDAi)(TrDAj ) (1 ≤ i,j ≤ 2).
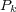
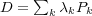
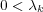
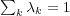
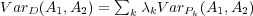
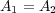
The main result in this work is that there are projections Pk such that ∑ D = kλkPk with 0 < λk and ∑ kλk = 1 and ∑ V arD(A1,A2) = k λkVarPk(A1,A2) . In a previous paper only the A1 = A2 case was included and the relevance is motivated by the paper [8].

2000 AMS Mathematics Subject Classification: Primary: 62J10; Secondary: 62F30.

Keywords and phrases: Density matrix, variance, covariance, decomposition, projections.Marekċ Częysóołwski

Download:    Abstract    Full text   Abstract + References