CONTRACTIONS AND CENTRAL EXTENSIONS OF QUANTUM WHITE
NOISE LIE ALGEBRAS
Luigi Accardi
Andreas Boukas
Abstract: We show that the Renormalized Powers of Quantum White Noise Lie algebra
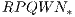 , with the convolution type renormalization
, with the convolution type renormalization 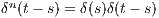 of the
of the
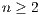 powers of the Dirac delta function, can be obtained through a contraction of the
Renormalized Powers of Quantum White Noise Lie algebra
powers of the Dirac delta function, can be obtained through a contraction of the
Renormalized Powers of Quantum White Noise Lie algebra 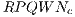 with the scalar
renormalization
with the scalar
renormalization 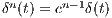 ,
, 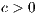 . Using this renormalization, we also obtain a Lie
algebra
. Using this renormalization, we also obtain a Lie
algebra 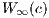 which contains the
which contains the 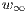 Lie algebra of Bakas and the Witt algebra as
contractions. Motivated by the
Lie algebra of Bakas and the Witt algebra as
contractions. Motivated by the 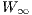 algebra of Pope, Romans and Shen, we show that
algebra of Pope, Romans and Shen, we show that
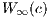 can also be centrally extended in a non-trivial fashion. In the case of the Witt
subalgebra of
can also be centrally extended in a non-trivial fashion. In the case of the Witt
subalgebra of 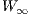 , the central extension coincides with that of the Virasoro algebra.
, the central extension coincides with that of the Virasoro algebra.
2000 AMS Mathematics Subject Classification: Primary: 60B15; Secondary:
60H40.
Keywords and phrases: Contraction of a Lie algebra, renormalized powers of quantum
white noise, Virasoro algebra, 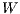 -algebras.
-algebras.