UNIVERSITY
OF WROCŁAW
 
Main Page
Contents
Online First
General Information
Instructions for authors


VOLUMES
43.2 43.1 42.2 42.1 41.2 41.1 40.2
40.1 39.2 39.1 38.2 38.1 37.2 37.1
36.2 36.1 35.2 35.1 34.2 34.1 33.2
33.1 32.2 32.1 31.2 31.1 30.2 30.1
29.2 29.1 28.2 28.1 27.2 27.1 26.2
26.1 25.2 25.1 24.2 24.1 23.2 23.1
22.2 22.1 21.2 21.1 20.2 20.1 19.2
19.1 18.2 18.1 17.2 17.1 16.2 16.1
15 14.2 14.1 13.2 13.1 12.2 12.1
11.2 11.1 10.2 10.1 9.2 9.1 8
7.2 7.1 6.2 6.1 5.2 5.1 4.2
4.1 3.2 3.1 2.2 2.1 1.2 1.1
 
 
WROCŁAW UNIVERSITY
OF SCIENCE AND
TECHNOLOGY

Contents of PMS, Vol. 35, Fasc. 2,
pages 201 - 222
 

SUPREMUM DISTRIBUTION OF BESSEL PROCESS OF DRIFTING BROWNIAN MOTION

Andrzej Pyć
Grzegorz Serafin
Tomasz Żak

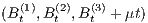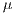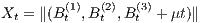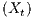Abstract: Let us assume that (B (1),B(2),B (3)+ μt) t t t is a three-dimensional Brownian motion with drift μ , starting at the origin. Then (1) (2) (3) Xt = ∥(B t ,Bt ,Bt + μt)∥ , its distance from the starting point, is a diffusion with many applications. We investigate the supremum of (Xt) , give an infinite-series formula for its distribution function and an exact estimate of the density of this distribution in terms of elementary functions.

2000 AMS Mathematics Subject Classification: Primary: 60J60; Secondary: 60G70.

Keywords and phrases: Drifting Brownian motion, Bessel process, supremum distribution, estimates of theta function.

Download:    Abstract    Full text   Abstract + References