SHARP INEQUALITIES FOR THE HAAR SYSTEM AND MARTINGALE
TRANSFORMS
Abstract: A classical result of Paley and Marcinkiewicz asserts that the Haar system on ![[0,1]](files/36.1/HTML/36.1.11.abs0x.png) forms an unconditional basis in
forms an unconditional basis in 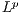 provided
provided 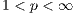 . The purpose of the paper is to
study related weak-type inequalities, which can be regarded as a version of this property for
. The purpose of the paper is to
study related weak-type inequalities, which can be regarded as a version of this property for
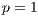 . Probabilistic counterparts, leading to some sharp estimates for martingale transforms,
are presented.
. Probabilistic counterparts, leading to some sharp estimates for martingale transforms,
are presented.
2000 AMS Mathematics Subject Classification: Primary: 60G42; Secondary:
60G46.
Keywords and phrases: Haar system, martingale, weak-type inequality, Bellman
function, best constants.