W rozdziale 4 zdefiniowaliśmy rząd przekształcenia liniowego
![]() jako
jako
![]() . Załóżmy, że
. Załóżmy, że
![]() i
i
![]() są bazami przestrzeni
są bazami przestrzeni
![]() i
i ![]() odpowiednio. Niech
odpowiednio. Niech
![]() będzie
izomorfizmem danym przez
będzie
izomorfizmem danym przez
![]() . Wynika stąd, że
. Wynika stąd, że
![]() .
.
Na mocy uwagi 4.11, wektory
![]() generują
generują ![]() ,
więc ich obrazy względem
,
więc ich obrazy względem ![]() , tzn. wektory
, tzn. wektory
![]() , generują
, generują
![]() . Wektory te to kolumny macierzy
. Wektory te to kolumny macierzy
![]() .
Zatem
.
Zatem
![]()
![]() liczba liniowo
niezależnych kolumn macierzy
liczba liniowo
niezależnych kolumn macierzy
![]() .
.
Dlatego przyjmujemy następującą definicję.
Problem. Jak praktycznie obliczyć rząd macierzy ?
By rozwiązać ten problem, udowodnimy najpierw następujące twierdzenie.
1) Pokażemy najpierw, że ![]() . Wybierzmy liniowo niezależne
wiersze
. Wybierzmy liniowo niezależne
wiersze
![]() . Utwórzmy z tych wierszy macierz
. Utwórzmy z tych wierszy macierz
![\begin{displaymath}B=\left[\begin{array}{c}R_{i_1} \vdots\\
R_{i_r}\end{array}\right]\end{displaymath}](img965.png)
![\begin{displaymath}X=\left[\begin{array}{c}x_1 \vdots x_n\end{array}\right]\...
...array}{c}R_1\cdot X=0 \vdots R_n\cdot
X=0\end{array}\right.\end{displaymath}](img971.png)
![\begin{displaymath}\iff\left\{\begin{array}{c}R_{i_1}\cdot X=0 \vdots R{i_r}...
...y}{c}x_1 \vdots\\
x_n\end{array}\right]=0\iff X\in Ker(F_B).\end{displaymath}](img973.png)
Jednak z drugiej strony
![]() (bo
(bo
![]() ),
więc
),
więc
![]() .
.
2) Powtarzając powyższe rozumowanie dla macierzy transponowanej
![]() dostajemy
dostajemy ![]() . Dlatego
. Dlatego ![]() .
.
![]() Załóżmy, że
Załóżmy, że
![]() . Na mocy twierdzenia
7.3, możemy wybrać liniowo niezależne wiersze
. Na mocy twierdzenia
7.3, możemy wybrać liniowo niezależne wiersze
![]() . Podobnie jak w dowodzie twierdzenia 7.3
tworzymy z tych wierszy macierz
. Podobnie jak w dowodzie twierdzenia 7.3
tworzymy z tych wierszy macierz ![]() wymiaru
wymiaru ![]() , o kolumnach
, o kolumnach
![]() . Zauważmy, że kolumny te są odpowiednimi
fragmentami kolumn
. Zauważmy, że kolumny te są odpowiednimi
fragmentami kolumn ![]() .
.
Na mocy twierdzenia 7.3 możemy wybrać liniowo niezależne kolumny
![]() . Tworzą one macierz
. Tworzą one macierz
![]() wymiaru
wymiaru ![]() , więc na mocy wniosku 4.14 i twierdzenia 5.13,
, więc na mocy wniosku 4.14 i twierdzenia 5.13,
![]() Załóżmy, że po wyborze pewnych
Załóżmy, że po wyborze pewnych ![]() wierszy
wierszy
![]() i
i ![]() kolumn
kolumn ![]() powstanie macierz
powstanie macierz
![]() o wyznaczniku
o wyznaczniku ![]() (tzn. niezerowy
minor). Znaczy to, że kolumny
(tzn. niezerowy
minor). Znaczy to, że kolumny
![]() są liniowo
niezależne.
są liniowo
niezależne.
Pokażemy, że kolumny
![]() też są liniowo
niezależne, dowodząc tym samym, że
też są liniowo
niezależne, dowodząc tym samym, że
![]() .
.
Istotnie, zauważmy, że kolumny ![]() są odpowiednimi
fragmentami kolumn
są odpowiednimi
fragmentami kolumn ![]() . Dlatego jeśli dla pewnych
. Dlatego jeśli dla pewnych ![]() mamy
mamy
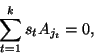
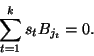
Widzimy więc, że dla obliczenia rzędu macierzy wystarczy obliczyć liczbę liniowo niezależnych wierszy. Poznamy teraz pewien szczególny rodzaj macierzy, dla ktorych jest to bardzo łatwe.
Przykład Poniższa macierz ma uporządkowane wiersze.
![\begin{displaymath}\left[\begin{array}{ccccc}1&0&2&0&0 0&0&1&0&1 0&0&0&2&2\\
0&0&0&0&0\end{array}\right].\end{displaymath}](img1010.png)
Zauważmy, że rząd macierzy z uporządkowanymi wierszami ![]() liczba
liniowo niezależnych wierszy
liczba
liniowo niezależnych wierszy ![]() liczba niezerowych wierszy.
liczba niezerowych wierszy.
Używając operacji z faktu 7.7 (w istocie wystarcza operacja (2)) możemy każdą macierz sprowadzić do postaci z uporządkowanymi wierszami i w ten sposób obliczyć jej rząd.
Przykład
Obliczymy rząd macierzy
![\begin{displaymath}A=\left[\begin{array}{cccc}1&2&3&1 2&1&2&0\\
3&3&5&1\end{array}\right].\end{displaymath}](img1013.png)
![\begin{displaymath}\left[\begin{array}{cccc}1&2&3&1 2&1&2&0\\
3&3&5&1\end{arr...
...ight]\!\!\!\begin{array}{l}\mbox{}\\
\mbox{} -[2]\end{array}\end{displaymath}](img1014.png)
![\begin{displaymath}\longrightarrow\left[\begin{array}{rrrr}1&2&3&1 0&-3&-4&-2\\
0&0&0&0\end{array}\right].\end{displaymath}](img1015.png)
Zastosowania.
1. Niech
![]() . Wówczas
. Wówczas
![]() rząd macierzy
rząd macierzy
![]() , który możemy już łatwo
obliczyć.
, który możemy już łatwo
obliczyć.
2. Niech
![]() będzie bazą przestrzeni liniowej
będzie bazą przestrzeni liniowej ![]() oraz
oraz
![]() . Wówczas używając izomorfizmu
liniowego między
. Wówczas używając izomorfizmu
liniowego między ![]() i
i
![]() dostajemy, że
dostajemy, że
W następnej uwadze podamy własności rzędu macierzy.
Na mocy faktu 7.2,
![]() i
i
![]() . Mamy
. Mamy
By dowieść, że
![]() , rozważmy bazę
, rozważmy bazę ![]() podprzestrzeni
podprzestrzeni
![]() . Wtedy zbiór
. Wtedy zbiór ![]() generuje
przestrzeń
generuje
przestrzeń
![]() (uwaga 4.11). Dlatego
(uwaga 4.11). Dlatego
2)
![]() , więc na mocy (1),
, więc na mocy (1),
Dowód (3) jest podobny.
Załóżmy, że przestrzeń ![]() ma wymiar skończony oraz
ma wymiar skończony oraz
![]() jest liniowe. Macierz
jest liniowe. Macierz ![]() w dowolnej bazie
przestrzeni
w dowolnej bazie
przestrzeni ![]() umożliwia nam wyliczanie obrazów wektorów przy
przekształceniu
umożliwia nam wyliczanie obrazów wektorów przy
przekształceniu ![]() . Jednak obliczenia przy użyciu macierzy mogą
być żmudne. Dlatego staramy się często znaleźć taką bazę
. Jednak obliczenia przy użyciu macierzy mogą
być żmudne. Dlatego staramy się często znaleźć taką bazę ![]() przestrzeni
przestrzeni ![]() , by macierz
, by macierz
![]() była możliwie najprostsza,
najlepiej diagonalna, tzn. postaci
była możliwie najprostsza,
najlepiej diagonalna, tzn. postaci
![\begin{displaymath}\left[\begin{array}{cccc}a_1&0&\cdots&0 0& a_2&\cdots&0\\
\mbox{}&\mbox{}&\ddots&\mbox{} 0&0&\cdots&a_n\end{array}\right].\end{displaymath}](img1038.png)
Problem. Czy istnieje baza ![]() przestrzeni
przestrzeni ![]() taka, że
macierz
taka, że
macierz ![]() jest diagonalna ?
jest diagonalna ?
By rozwiązać ten problem, wprowadzamy następującą definicję.
Definicję macierzy diagonalizowalnej uzasadnia twierdzenie 7.11 poniżej. W jego dowodzie będziemy potrzebowali następującego lematu.
2) Definiujemy wektory
![]() następującymi wzorami.
następującymi wzorami.
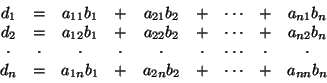
![\begin{displaymath}\left[\begin{array}{c}d_1 d_2 \vdots\\
d_n\end{array}\ri...
...ft[\begin{array}{c}b_1 b_2\\
\vdots b_n\end{array}\right].\end{displaymath}](img1049.png)
![\begin{displaymath}\left[\begin{array}{c}b_1 b_2 \vdots\\
b_n\end{array}\ri...
...ft[\begin{array}{c}d_1 d_2\\
\vdots d_n\end{array}\right].\end{displaymath}](img1050.png)
1) Definiujemy wektory
![]() tak, że
tak, że
![\begin{displaymath}\left[\begin{array}{c}c_1 c_2 \vdots\\
c_n\end{array}\ri...
...ft[\begin{array}{c}b_1 b_2\\
\vdots b_n\end{array}\right],\end{displaymath}](img1054.png)
![\begin{displaymath}\left[\begin{array}{c}b_1 b_2 \vdots\\
b_n\end{array}\ri...
...ft[\begin{array}{c}c_1 c_2\\
\vdots c_n\end{array}\right].\end{displaymath}](img1055.png)
![]() . Niech
. Niech ![]() będzie bazą
będzie bazą ![]() taką, że
taką, że
![]() jest diagonalna. Wtedy na mocy uwagi 6.6,
jest diagonalna. Wtedy na mocy uwagi 6.6,
![]() Załóżmy, że dla pewnej macierzy odwracalnej
Załóżmy, że dla pewnej macierzy odwracalnej ![]() macierz
macierz ![]() jest diagonalna. Na mocy lematu 7.10(1) istnieje
baza
jest diagonalna. Na mocy lematu 7.10(1) istnieje
baza ![]() przestrzeni
przestrzeni ![]() taka, że
taka, że
![]() i
i
![]() . Na mocy uwagi 6.6 macierz
. Na mocy uwagi 6.6 macierz
By rozstrzygnąć, czy dane przekształcenie ![]() lub macierz
lub macierz ![]() są
diagonalizowalne, będziemy potrzebowali kilku nowych pojęć.
są
diagonalizowalne, będziemy potrzebowali kilku nowych pojęć.
![\begin{displaymath}(*) m_{{\cal B}{\cal B}}(F)=\left[\begin{array}{cccc}t_1&0...
...ox{}&\mbox{}&\ddots&\mbox{}\\
0&0&\cdots&t_n\end{array}\right]\end{displaymath}](img1068.png)
![]() Załóżmy, że
Załóżmy, że ![]() jest diagonalizowalne, tzn. dla
pewnej bazy
jest diagonalizowalne, tzn. dla
pewnej bazy
![]() przestrzeni
przestrzeni ![]() macierz
macierz ![]() w tej
bazie jest diagonalna, czyli jest postaci
w tej
bazie jest diagonalna, czyli jest postaci ![]() . Zwróćmy uwagę, że
wówczas wszystkie wektory bazy
. Zwróćmy uwagę, że
wówczas wszystkie wektory bazy ![]() są wektorami własnymi
przekształcenia
są wektorami własnymi
przekształcenia ![]() (dla kolejnych wartości własnych
(dla kolejnych wartości własnych
![]() ).
).
Przykład. Nie każde przekształcenie liniowe jest
diagonalizowalne. Na przykład obrót
![]() wokół
wokół ![]() , o kąt
, o kąt
![]() nie jest diagonalizowalny, bo
nie ma żadnych wektorów własnych.
nie jest diagonalizowalny, bo
nie ma żadnych wektorów własnych.
W następnym rozdziale zajmiemy się problemem, jak znaleźć wektory
własne i wartości własne ![]() .
.