Next: 9. Relacje równoważności, funkcje
Up: Wstęp do matematyki
Previous: 7. Rachunek kwantyfikatorów
Potocznie mówimy, że zbiór skończony 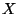 jest w uporządkowany, gdy
jego elementy możemy ułożyć w szereg od ``najmniejszego''
do ``największego''. Dla określenia takiego porządku istotna jest
relacja ``
jest w uporządkowany, gdy
jego elementy możemy ułożyć w szereg od ``najmniejszego''
do ``największego''. Dla określenia takiego porządku istotna jest
relacja ``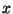 poprzedza
poprzedza 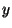 '', którą często symbolicznie zapisujemy
w postaci
'', którą często symbolicznie zapisujemy
w postaci 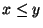 . Taka relacja porządku
. Taka relacja porządku 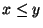 jest określona
na zbiorze liczb rzeczywistych
jest określona
na zbiorze liczb rzeczywistych 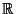 . Analizując jej własności
formułujemy ogólną definicję.
. Analizując jej własności
formułujemy ogólną definicję.
Definicja 8.1
Załóżmy, że
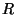
jest relacją na zbiorze
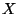
oraz
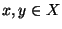
.
(1) Relacja 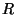 na zbiorze
na zbiorze 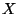 jest relacją liniowego
porządku (lub krócej: liniowym porządkiem), gdy jest zwrotna, przechodnia, antysymetryczna i spójna.
jest relacją liniowego
porządku (lub krócej: liniowym porządkiem), gdy jest zwrotna, przechodnia, antysymetryczna i spójna.
(2) Jeśli relacja 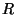 ma trzy pierwsze własności, nazywamy ją
relacją częściowego porządku (lub krócej: częściowym
porządkiem).
ma trzy pierwsze własności, nazywamy ją
relacją częściowego porządku (lub krócej: częściowym
porządkiem).
Załóżmy, że 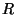 jest częściowym porządkiem na zbiorze
jest częściowym porządkiem na zbiorze 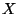 .
.
(3) Gdy
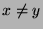 i
i 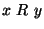 , mówimy, że
, mówimy, że
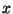 jest mniejszy od
jest mniejszy od 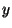 (poprzedza
(poprzedza 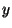 ) i
) i 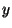 jest większy od
jest większy od 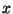 (w
sensie częściowego porządku
(w
sensie częściowego porządku 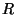 ). Dodatkowo, jeśli nie istnieje
element
). Dodatkowo, jeśli nie istnieje
element 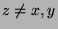 taki, że
taki, że 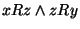 , to mówimy, że
, to mówimy, że 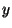 jest
następnikiem
jest
następnikiem 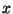 , zaś
, zaś 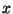 poprzednikiem
poprzednikiem 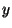 .
.
(4) Mówimy, że elementy 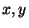 są
porównywalne w tym częściowym porządku, gdy
są
porównywalne w tym częściowym porządku, gdy 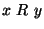 lub
lub
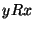 .
.
Widzimy więc, że w częściowym porządku nie zawsze wszystkie elementy są
porównywalne, w przeciwieństwie do liniowego porządku, gdzie
spójność gwarantuje porównywalność każdych dwóch elementów.
Przykład liniowego porządku to relacja 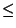 na
na 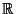 . Każdy
liniowy porządek jest w szczególności częściowy. Przykład
częściowego porządku, który nie jest liniowy, to relacja
podzielności na zbiorze
. Każdy
liniowy porządek jest w szczególności częściowy. Przykład
częściowego porządku, który nie jest liniowy, to relacja
podzielności na zbiorze 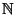 czy też relacja inkluzji
czy też relacja inkluzji
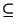 na zbiorze
na zbiorze 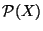 .
.
Relacje porządku często oznacza się symbolem 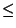 lub symbolami podobnymi.
lub symbolami podobnymi.
Uwaga 8.2
Jeśli
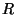
jest relacją częściowego [odpowiednio: liniowego] porządku na
zbiorze
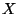
, to dla
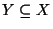
relacja ograniczona
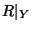
również jest porządkiem częściowym [odpowiednio: liniowym].
Relacje porządku na zbiorze skończonym wygodnie jest przedstawiać w
formie graficznej, w postaci diagramów Hassego. Diagram Hassego składa się z pewnej liczby punktów
odpowiadających elementom naszego zbioru. Pary punktów odpowiadające
parom (poprzednik, następnik) są połączone
niepoziomymi odcinkami. Element 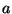 jest mniejszy od elementu
jest mniejszy od elementu 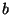 dokładnie
wtedy, gdy na rysunku można dojść od punktu odpowiadającego
elementowi
dokładnie
wtedy, gdy na rysunku można dojść od punktu odpowiadającego
elementowi 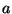 do punktu odpowiadającego elementowi
do punktu odpowiadającego elementowi 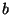 wzdłuż
odcinków idąc cały czas w górę.
wzdłuż
odcinków idąc cały czas w górę.
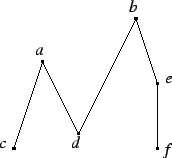
Przykład 1. Niech
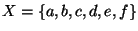 . Na rysunku
. Na rysunku
przedstawiona jest relacja
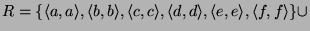
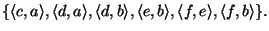 Oznaczając relację
Oznaczając relację 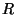 symbolem
symbolem 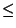 mamy więc:
mamy więc:
Relacja ta jest częściowym porządkiem, nie jest jednak liniowym
porządkiem, gdyż nie jest spójna (np. 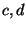 nie są porównywalne).
nie są porównywalne).
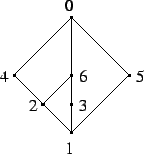
Przykład 2. Rysunek
określa liniowy porządek 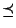 na zbiorze
na zbiorze
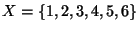 taki, że
taki, że
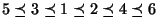 i ogólniej liczba napisana niżej
jest mniejsza od liczby napisanej wyżej. Oczywiście
i ogólniej liczba napisana niżej
jest mniejsza od liczby napisanej wyżej. Oczywiście 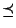 różni się od zwykłego porządku
różni się od zwykłego porządku 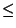 na zbiorze
na zbiorze 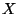 .
.
Przykład 3. Niech
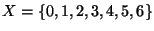 . Rysunek
. Rysunek
przedstawia relację podzielności 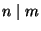 , która jest częściowym
porządkiem na zbiorze
, która jest częściowym
porządkiem na zbiorze 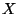 (jako ograniczenie relacji
(jako ograniczenie relacji 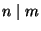 na
zbiorze
na
zbiorze 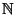 do zbioru
do zbioru 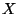 ).
).
W przykładzie 1. elementy 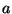 i
i 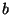 są maksymalne, elementy
są maksymalne, elementy 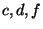 są minimalne, nie ma ani elementów największych ani najmniejszych.
są minimalne, nie ma ani elementów największych ani najmniejszych.
W przykładzie 2. 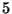 jest elementem najmniejszym i jedynym elementem
minimalnym,
jest elementem najmniejszym i jedynym elementem
minimalnym, 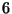 jest elementem największym i jedynym elementem
maksymalnym.
jest elementem największym i jedynym elementem
maksymalnym.
W przykładzie 3. 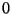 jest elementem największym i jedynym
maksymalnym, zaś
jest elementem największym i jedynym
maksymalnym, zaś 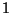 elementem najmniejszym i jedynym minimalnym.
elementem najmniejszym i jedynym minimalnym.
Uwaga 8.4 (1)
Jeśli
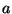
jest największy, to
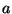
jest
maksymalny.
(2) Jeśli
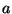
jest najmniejszy, to
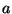
jest minimalny.
(3) Jeśli w
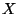
istnieje element największy, to jest on jedyny,
ponadto w tym przypadku jest on również jedynym elementem
maksymalnym.
(4) Jeśli w
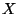
istnieje element najmniejszy, to jest on jedyny,
ponadto w tym przypadku jest on również jedynym elementem minimalnym.
Dowód. (1) Załóżmy, że 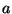 jest największy. Jest więc
większy w sensie
jest największy. Jest więc
większy w sensie 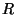 od wszystkich innych elementów
od wszystkich innych elementów 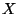 . Dlatego nie
ma w
. Dlatego nie
ma w 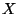 elementu większego od
elementu większego od 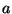 w sensie
w sensie 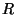 . To potoczne
rozumowanie może być jednak mylące, gdyż może być odczytywane w
oparciu o nieadekwatne w tym przypadku intuicje na temat liniowego porządku
liczb rzeczywistych (tzn. czytelnik może być nieświadom, gdzie w dowodzie
używa się własności częściowego porządku). Dlatego przeprowadzimy dowód bardziej formalnie.
. To potoczne
rozumowanie może być jednak mylące, gdyż może być odczytywane w
oparciu o nieadekwatne w tym przypadku intuicje na temat liniowego porządku
liczb rzeczywistych (tzn. czytelnik może być nieświadom, gdzie w dowodzie
używa się własności częściowego porządku). Dlatego przeprowadzimy dowód bardziej formalnie.
Załóżmy więc jeszcze raz, że 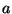 jest największy, tzn.
jest największy, tzn.
- (a)
- dla
każdego
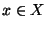 mamy
mamy 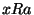 .
.
By pokazać, że 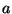 jest maksymalny,
musimy udowodnić, że
jest maksymalny,
musimy udowodnić, że
czyli że
- (b)
- dla każdego
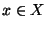 , jeżeli
, jeżeli 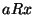 , to
, to 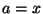 .
.
W tym celu rozważamy dowolne 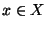 . Zakładając, że
. Zakładając, że 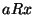 , chcemy
pokazać, że
, chcemy
pokazać, że 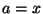 (tzn. chcemy pokazać prawdziwość implikacji
(tzn. chcemy pokazać prawdziwość implikacji
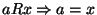 ). Przypuśćmy więc, że
). Przypuśćmy więc, że 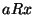 . Z punktu (a)
dostajemy też, że
. Z punktu (a)
dostajemy też, że 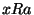 . Warunek antysymetryczności daje nam, że
. Warunek antysymetryczności daje nam, że 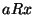 i
i
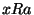 implikuje
implikuje 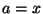 . Dlatego mamy
. Dlatego mamy 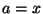 , co kończy dowód (b) i
(1).
, co kończy dowód (b) i
(1).
Dowody pozostałych punktów pozostawiamy jako ćwiczenie. 
Załóżmy teraz, że 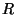 jest liniowym porządkiem na zbiorze
skończonym
jest liniowym porządkiem na zbiorze
skończonym 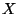 . Rozumując podobnie jak w dowodzie uwagi 8.4
można udowodnić, że wtedy istnieją w
. Rozumując podobnie jak w dowodzie uwagi 8.4
można udowodnić, że wtedy istnieją w 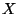 elementy największe i
najmniejsze (na mocy uwagi 8.4 są one jedyne). Wybieramy więc
kolejno
elementy największe i
najmniejsze (na mocy uwagi 8.4 są one jedyne). Wybieramy więc
kolejno 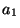 jako element najmniejszy w
jako element najmniejszy w 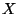 ,
, 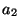 jako element
najmniejszy w zbiorze
jako element
najmniejszy w zbiorze
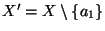 (względem relacji
(względem relacji
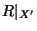 ),
), 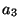 jako element najmniejszy w zbiorze
jako element najmniejszy w zbiorze
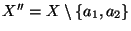 (względem relacji
(względem relacji 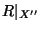 ), i tak
dalej. W ten sposób po skończeniu wielu krokach wyczerpiemy zbiór
), i tak
dalej. W ten sposób po skończeniu wielu krokach wyczerpiemy zbiór
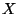 układając jego elementy w uporządkowany (w sensie
układając jego elementy w uporządkowany (w sensie 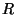 ) szereg
) szereg
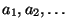 , od najmniejszego do największego. W szeregu tym
elementy wcześniejsze będą mniejsze w sensie
, od najmniejszego do największego. W szeregu tym
elementy wcześniejsze będą mniejsze w sensie 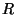 od elementów
późniejszych (na mocy przechodniości). Odpowiada to dobrze intuicji związanej ze zwykłym liniowym
uporządkowaniem liczb rzeczywistych. Uzasadnia to poprawność naszej
definicji liniowego porządku.
od elementów
późniejszych (na mocy przechodniości). Odpowiada to dobrze intuicji związanej ze zwykłym liniowym
uporządkowaniem liczb rzeczywistych. Uzasadnia to poprawność naszej
definicji liniowego porządku.
Definicja 8.5
Załóżmy, że
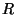
jest częściowym porządkiem na
zbiorze
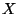
,
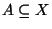
i
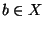
.
 jest łańcuchem
jest łańcuchem
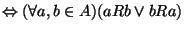
(Jest to warunek spójności, jedyny brakujący do tego, by 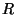 była
liniowym porządkiem, dlatego też w tym przypadku warunek ten jest
równoważny temu, że
była
liniowym porządkiem, dlatego też w tym przypadku warunek ten jest
równoważny temu, że 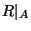 jest liniowym porządkiem.)
jest liniowym porządkiem.)
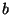 jest ograniczeniem górnym zbioru
jest ograniczeniem górnym zbioru
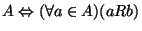
(tzn. 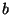 jest równe lub większe (w sensie
jest równe lub większe (w sensie 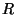 ) od
wszystkich elementów
) od
wszystkich elementów  ).
).
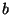 jest ograniczeniem dolnym zbioru
jest ograniczeniem dolnym zbioru
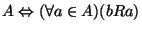
(tzn. 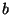 jest równe lub mniejsze (w sensie
jest równe lub mniejsze (w sensie 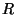 ) od
wszystkich elementów
) od
wszystkich elementów  ).
).
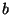 jest kresem górnym zbioru
jest kresem górnym zbioru
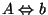 jest
najmniejszym ograniczeniem górnym zbioru
jest
najmniejszym ograniczeniem górnym zbioru  .
.
Symbolicznie warunek ten można zapisać następująco:
Mówi on po pierwsze, że 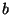 jest ograniczeniem górnym zbioru
jest ograniczeniem górnym zbioru  , a
następnie, że dla dowolnego
, a
następnie, że dla dowolnego 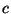 , jeśli
, jeśli 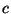 jest ograniczeniem górnym
jest ograniczeniem górnym
 , to
, to 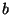 jest mniejsze lub równe
jest mniejsze lub równe 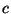 (w sensie
(w sensie
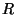 )8.1.
)8.1.
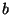 jest kresem dolnym zbioru
jest kresem dolnym zbioru
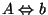 jest
największym ograniczeniem dolnym zbioru
jest
największym ograniczeniem dolnym zbioru  (względem
(względem
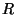 )8.2.
)8.2.
Badanie istnienia ograniczeń i kresów zbioru  wymaga często nieco wysiłku.
wymaga często nieco wysiłku.
Przykład 4. Rozważmy znów relację podzielności 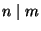 na
zbiorze
na
zbiorze 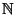 . Zbiór
. Zbiór
złożony z 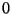 i kolejnych potęg dwójki
jest łańcuchem w tym częściowym porządku. Istotnie, jest on
liniowo uporządkowany przez relację podzielności. Zbadamy istnienie
ograniczeń i kresów górnych i dolnych.
i kolejnych potęg dwójki
jest łańcuchem w tym częściowym porządku. Istotnie, jest on
liniowo uporządkowany przez relację podzielności. Zbadamy istnienie
ograniczeń i kresów górnych i dolnych.
Ograniczenia dolne. Liczba naturalna 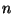 jest ograniczeniem
dolnym zbioru
jest ograniczeniem
dolnym zbioru  (w sensie relacji podzielności) dokładnie wtedy,
gdy dla wszystkich
(w sensie relacji podzielności) dokładnie wtedy,
gdy dla wszystkich 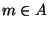 mamy
mamy 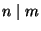 , tzn. gdy
, tzn. gdy 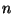 dzieli
wszystkie liczby ze zbioru
dzieli
wszystkie liczby ze zbioru  . Widzimy, że jedyna taka liczba
. Widzimy, że jedyna taka liczba 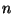 to
to
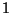 . Zatem
. Zatem 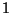 jest jedynym ograniczeniem dolnym zbioru
jest jedynym ograniczeniem dolnym zbioru  , jest w
związku z tym największym (w sensie relacji podzielności) takim
ograniczeniem czyli jest kresem dolnym zbioru
, jest w
związku z tym największym (w sensie relacji podzielności) takim
ograniczeniem czyli jest kresem dolnym zbioru  .
.
Ograniczenia górne. Liczba naturalna 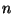 jest ograniczeniem
górnym zbioru
jest ograniczeniem
górnym zbioru  ( w sensie relacji podzielności) dokładnie wtedy, gdy dzieli się przez wszystkie
liczby ze zbioru
( w sensie relacji podzielności) dokładnie wtedy, gdy dzieli się przez wszystkie
liczby ze zbioru  . Widzimy, że jedyną taką liczbą
. Widzimy, że jedyną taką liczbą 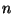 jest
jest
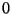 . Jest więc ona także kresem górnym zbioru
. Jest więc ona także kresem górnym zbioru  .
.
Przykład 5. Rozważmy zwykły porządek 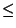 na zbiorze
liczb rzeczywistych
na zbiorze
liczb rzeczywistych 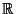 . Jest to liniowy porządek, więc zarówno
zbiór
. Jest to liniowy porządek, więc zarówno
zbiór 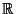 , jak i jego każdy podzbiór, jest tu
łańcuchem. Niech
, jak i jego każdy podzbiór, jest tu
łańcuchem. Niech
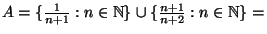
Znajdziemy kresy dolny i górny zbioru  .
.
Ograniczenia dolne. Niech
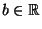 . Dowodzimy, że
. Dowodzimy, że 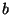 jest
ograniczeniem dolnym zbioru
jest
ograniczeniem dolnym zbioru
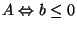 .
.
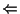 . Załóżmy, że
. Załóżmy, że 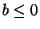 . Wtedy oczywiście
. Wtedy oczywiście 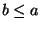 dla wszystkich
dla wszystkich 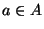 , gdyż wszystkie liczby ze zbioru
, gdyż wszystkie liczby ze zbioru  są
są
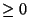 . Zatem
. Zatem 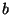 jest ograniczeniem dolnym zbioru
jest ograniczeniem dolnym zbioru  .
.
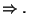 Nie wprost. Przypuśćmy, że
Nie wprost. Przypuśćmy, że 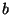 jest ograniczeniem
dolnym zbioru
jest ograniczeniem
dolnym zbioru  oraz nieprawda, że
oraz nieprawda, że 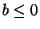 , to znaczy mamy
, to znaczy mamy
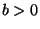 . Korzystając z własności liczb
rzeczywistych8.3znajdujemy liczbę naturalną
. Korzystając z własności liczb
rzeczywistych8.3znajdujemy liczbę naturalną 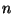 taką, że
taką, że
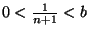 . Ale
. Ale
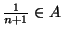 , więc
skoro
, więc
skoro 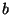 ogranicza z dołu zbiór
ogranicza z dołu zbiór  , to
, to
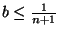 . Uzyskana sprzeczność kończy dowód
. Uzyskana sprzeczność kończy dowód 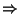 .
.
Widzimy, że w zbiorze ograniczeń dolnych zbioru  istnieje liczba
największa: jest to
istnieje liczba
największa: jest to 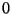 . Dlatego
. Dlatego 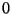 jest kresem dolnym zbioru
jest kresem dolnym zbioru  .
.
Podobnie pokazujemy, że 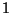 jest kresem górnym zbioru
jest kresem górnym zbioru
 . Szczegóły pozostawiamy jako ćwiczenie.
. Szczegóły pozostawiamy jako ćwiczenie.
Nasza definicja relacji liniowego porządku odzwierciedla własności
relacji 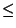 na
na 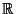 . Definiuje się również tak zwane relacje
ścisłego porządku liniowego (i częściowego), odpowiadające
własnościom relacji
. Definiuje się również tak zwane relacje
ścisłego porządku liniowego (i częściowego), odpowiadające
własnościom relacji 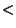 na
na 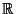 . Mianowicie, mówimy, że relacja
. Mianowicie, mówimy, że relacja
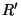 na zbiorze
na zbiorze 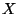 jest relacją ścisłego porządku liniowego, gdy
ma następujące własności:
jest relacją ścisłego porządku liniowego, gdy
ma następujące własności:
-
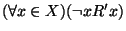 (przeciwzwrotność)
(przeciwzwrotność)
-
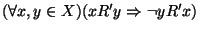 (ścisła
antysymetryczność)
(ścisła
antysymetryczność)
-
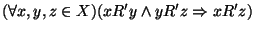 (przechodniość)
(przechodniość)
-
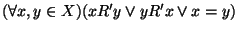 (ścisła
spójność).
(ścisła
spójność).
Gdy relacja 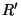 spełnia warunki 1-3, nazywamy ją ścisłym
częściowym porządkiem.
spełnia warunki 1-3, nazywamy ją ścisłym
częściowym porządkiem.
Następująca uwaga pokazuje związek między porządkami i ścisłymi
porządkami. Jej dowód opiera sie na spostrzeżeniu, że w przypadku
liczb rzeczywistych 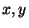 mamy
mamy
Uwaga 8.6
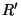
jest relacją ścisłego częściowego [odpowiednio: liniowego] porządku na
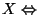
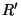
jest przeciwzwrotna i
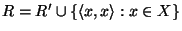
jest
relacją częściowego [odpowiednio: liniowego] porządku na
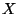
.



Next: 9. Relacje równoważności, funkcje
Up: Wstęp do matematyki
Previous: 7. Rachunek kwantyfikatorów
Ludomir Newelski
2005-09-22
![]() na zbiorze
na zbiorze ![]() jest relacją liniowego
porządku (lub krócej: liniowym porządkiem), gdy jest zwrotna, przechodnia, antysymetryczna i spójna.
jest relacją liniowego
porządku (lub krócej: liniowym porządkiem), gdy jest zwrotna, przechodnia, antysymetryczna i spójna.
![]() ma trzy pierwsze własności, nazywamy ją
relacją częściowego porządku (lub krócej: częściowym
porządkiem).
ma trzy pierwsze własności, nazywamy ją
relacją częściowego porządku (lub krócej: częściowym
porządkiem).
![]() jest częściowym porządkiem na zbiorze
jest częściowym porządkiem na zbiorze ![]() .
.
![]() i
i ![]() , mówimy, że
, mówimy, że
![]() jest mniejszy od
jest mniejszy od ![]() (poprzedza
(poprzedza ![]() ) i
) i ![]() jest większy od
jest większy od ![]() (w
sensie częściowego porządku
(w
sensie częściowego porządku ![]() ). Dodatkowo, jeśli nie istnieje
element
). Dodatkowo, jeśli nie istnieje
element ![]() taki, że
taki, że ![]() , to mówimy, że
, to mówimy, że ![]() jest
następnikiem
jest
następnikiem ![]() , zaś
, zaś ![]() poprzednikiem
poprzednikiem ![]() .
.
![]() są
porównywalne w tym częściowym porządku, gdy
są
porównywalne w tym częściowym porządku, gdy ![]() lub
lub
![]() .
.