Next: Arytmetyka liczb kardynalnych Up: Wstęp do matematyki Previous: (Przeciw)obrazy, ciągi
Widzimy, że równoliczność zbiorów ma własności relacji
równoważności. Czy jednak ![]() jest relacją równoważności ? W
ścisłym sensie nie, gdyż jej dziedzina i obraz nie są
zbiorami, nie istnieje bowiem zbiór wszystkich zbiorów. (Gdyby
bowiem taki zbiór
jest relacją równoważności ? W
ścisłym sensie nie, gdyż jej dziedzina i obraz nie są
zbiorami, nie istnieje bowiem zbiór wszystkich zbiorów. (Gdyby
bowiem taki zbiór ![]() istniał, to funkcja zdaniowa
istniał, to funkcja zdaniowa
![]() zdefiniowałaby nam zbiór z antynomii Russella.)
zdefiniowałaby nam zbiór z antynomii Russella.)
Jeśli jednak ograniczymy zakresy zmiennych ![]() i
i ![]() w funkcji
zdaniowej
w funkcji
zdaniowej ![]() do zbioru podzbiorów pewnej ustalonej
przestrzeni
do zbioru podzbiorów pewnej ustalonej
przestrzeni ![]() , to wówczas
, to wówczas ![]() staje się relacją
równoważności na zbiorze
staje się relacją
równoważności na zbiorze ![]() .
.
Intuicyjnie, liczba elementów zbioru ![]() (zwana inaczej mocą zbioru
(zwana inaczej mocą zbioru
![]() ) to wspólna własność wszystkich zbiorów równolicznych ze
zbiorem
) to wspólna własność wszystkich zbiorów równolicznych ze
zbiorem ![]() . Gdy ograniczamy
. Gdy ograniczamy ![]() do zbioru
do zbioru ![]() , dla
, dla
![]() moglibyśmy przyjąć (stosując zasadę abstrakcji), że moc
moglibyśmy przyjąć (stosując zasadę abstrakcji), że moc
![]() to po prostu klasa abstrakcji relacji
to po prostu klasa abstrakcji relacji ![]() . W ten sposób
wykluczylibyśmy jednak z rozważań zbiory równoliczne z
. W ten sposób
wykluczylibyśmy jednak z rozważań zbiory równoliczne z ![]() , które
nie zawierają się w przestrzeni
, które
nie zawierają się w przestrzeni ![]() .
.
W teorii mnogości rozwiązuje się ten problem nieco sztucznie:
tworzy się mianowicie dla wszystkich zbiorów ![]() pewne zbiory
oznaczane przez
pewne zbiory
oznaczane przez ![]() . Obiekty te mają następującą własność:
. Obiekty te mają następującą własność:
Dla dowolnych zbiorówW ten sposób grają one rolę ``nazw'' klas zbiorów równolicznych.mamy
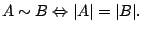
Liczby naturalne to po prostu liczby kardynalne zbiorów
skończonych. A więc na przykład, gdy zbiór ![]() jest
trzyelementowy, to
jest
trzyelementowy, to ![]() . W przypadku liczb naturalnych można
łatwo wyjaśnić, w jaki sposób są one konstruowane. Mianowicie w
teorii mnogości przyjmuje się, że
. W przypadku liczb naturalnych można
łatwo wyjaśnić, w jaki sposób są one konstruowane. Mianowicie w
teorii mnogości przyjmuje się, że
Niektóre inne liczby kardynalne mają specjalne nazwy i oznaczenia.
Przykładowo liczbę kardynalną
![]() oznacza się symbolem
oznacza się symbolem
![]() (czytaj: alef zero), zaś moc zbioru liczb rzeczywistych
nazywa się continuum i oznacza
mała gotycką literą
(czytaj: alef zero), zaś moc zbioru liczb rzeczywistych
nazywa się continuum i oznacza
mała gotycką literą ![]() . Podamy teraz przykłady zbiorów
równolicznych.
. Podamy teraz przykłady zbiorów
równolicznych.
Przykład 1. Niech
![]() .
. ![]() jest zbiorem
liczb parzystych. Są to zbiory równoliczne, świadczy o tym bijekcja
jest zbiorem
liczb parzystych. Są to zbiory równoliczne, świadczy o tym bijekcja
![]() dana wzorem
dana wzorem ![]() .
.
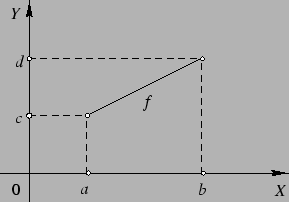
Przykład 4.
![]() , czyli przedziały otwarty i
domknięty są równoliczne. By to uzasadnić, znajdujemy bijekcję
, czyli przedziały otwarty i
domknięty są równoliczne. By to uzasadnić, znajdujemy bijekcję
![]() . Najpierw określamy pewien ciąg
różnowartościowy
. Najpierw określamy pewien ciąg
różnowartościowy ![]() liczb z
przedziału
liczb z
przedziału ![]() , na przykład niech
, na przykład niech
Niech ![]() . W rozwinięciu dziesiętnym liczba
. W rozwinięciu dziesiętnym liczba ![]() ma postać
ma postać
Niech
![]() . Widzimy, że
. Widzimy, że
![]() . Dlatego
. Dlatego
![]() i ogólniej
i ogólniej
![]() .
. ![]() jest różnowartościowa,
dlatego
jest różnowartościowa,
dlatego
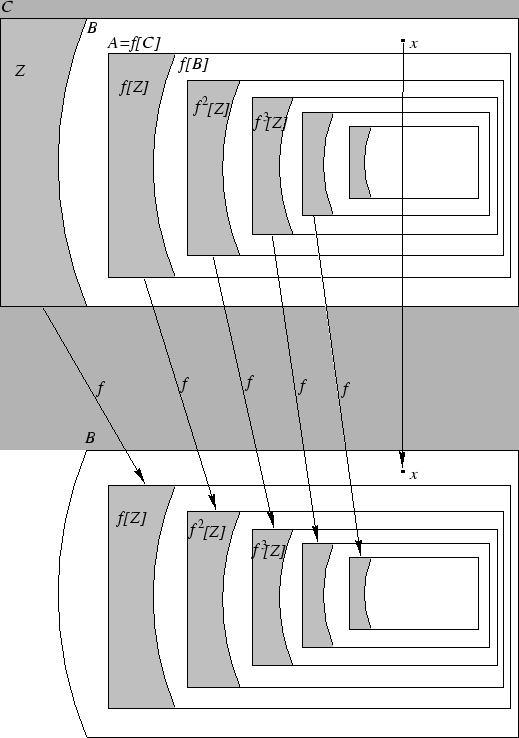
Przykład 6. Niech
![]() (jest to więc
``pełny kwadrat''). Wtedy zbiory
(jest to więc
``pełny kwadrat''). Wtedy zbiory ![]() i
i ![]() (z przykładu 5.) są
równoliczne.
By to uzasadnić, rozważmy jednokładność
(z przykładu 5.) są
równoliczne.
By to uzasadnić, rozważmy jednokładność ![]() płaszczyzny
płaszczyzny
![]() o środku w punkcie
o środku w punkcie
![]() i skali
i skali ![]() . Jest to bijekcja
płaszczyzny. Mamy
. Jest to bijekcja
płaszczyzny. Mamy
Zbiory przeliczalne.
Zatem zbiory przeliczalne to zbiór pusty, niepuste zbiory skończone i te zbiory nieskończone, które są równoliczne z
![]() . Jeśli
. Jeśli ![]() ma
ma ![]() elementów (
elementów (![]() ), to
), to
![]() dla pewnych
dla pewnych
![]() . Definiujemy
wtedy surjekcję
. Definiujemy
wtedy surjekcję
![]() wzorem:
wzorem:
![]() . Załóżmy, że
. Załóżmy, że
![]() jest
``na''. Wtedy
jest
``na''. Wtedy
![]() .
.
![]() . Załóżmy, że
. Załóżmy, że
![]() Gdy
Gdy
![]() jest skończony (wtedy ciąg
jest skończony (wtedy ciąg ![]() musi mieć powtórzenia), to
jest oczywiście przeliczalny. Załóżmy więc, że
musi mieć powtórzenia), to
jest oczywiście przeliczalny. Załóżmy więc, że ![]() jest
nieskończony. Wtedy w ciągu
jest
nieskończony. Wtedy w ciągu ![]() jest nieskończenie wiele
wyrazów. Skreślając w ciągu
jest nieskończenie wiele
wyrazów. Skreślając w ciągu
![]() te wyrazy, które wystąpiły już wcześniej, dostajemy nowy ciąg,
tym razem już bez powtórzeń. Ten nowy ciąg jest więc bijekcją
między
te wyrazy, które wystąpiły już wcześniej, dostajemy nowy ciąg,
tym razem już bez powtórzeń. Ten nowy ciąg jest więc bijekcją
między ![]() a
a ![]() .
. ![]()
Uwaga 11.7 tłumaczy nazwę zbioru przeliczalnego. Mianowicie, zbiór przeliczalny to taki zbiór, którego elementy możemy przeliczyć używając liczb naturalnych (być może wszystkich, gdy nasz zbiór jest nieskończony).
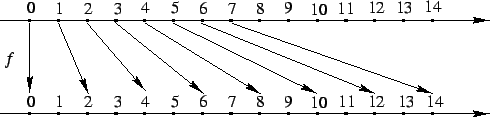
Przykład 1. Zbiór liczb całkowitych ![]() jest przeliczalny. Istotnie,
jest przeliczalny. Istotnie,
![]() .
.
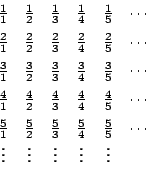
Przykład 2. Zbiór liczb wymiernych ![]() jest
przeliczalny. Może to być zaskakujące, że jest tyle samo liczb
wymiernych, co liczb naturalnych (tzn. że
jest
przeliczalny. Może to być zaskakujące, że jest tyle samo liczb
wymiernych, co liczb naturalnych (tzn. że
![]() ). By
to uzasadnić, najpierw układamy dodatnie liczby wymierne w
nieskończonej tablicy :
). By
to uzasadnić, najpierw układamy dodatnie liczby wymierne w
nieskończonej tablicy :
(2) Możemy wykreślić z ciągu zbiorów
![]() zbiory puste (nie wpływają one na sumę tych zbiorów). Jeśli
pozostanie tylko skończenie wiele zbiorów niewykreślonych, to ich
suma będzie przeliczalna na mocy kilkukrotnego zastosowania
(1). Dlatego możemy założyć, że pozostało nieskończenie
wiele zbiorów niewykreślonych.
zbiory puste (nie wpływają one na sumę tych zbiorów). Jeśli
pozostanie tylko skończenie wiele zbiorów niewykreślonych, to ich
suma będzie przeliczalna na mocy kilkukrotnego zastosowania
(1). Dlatego możemy założyć, że pozostało nieskończenie
wiele zbiorów niewykreślonych.
Zmieniając odpowiednio ich numerację możemy założyc, że
wszystkie zbiory ![]() są niepuste. Możemy zatem elementy każdego
zbioru
są niepuste. Możemy zatem elementy każdego
zbioru ![]() ustawić w ciąg:
ustawić w ciąg:

(3) Znów możemy założyć, że oba zbiory ![]() są niepuste oraz
są niepuste oraz
![]() i
i
![]() . Dla
. Dla
![]() niech
niech
![]() . Zatem zbiór
. Zatem zbiór ![]() składa się z tych par
składa się z tych par
![]() , dla których
, dla których ![]() .
Widzimy, że
.
Widzimy, że
![]() , jest więc
przeliczalny.
Ponadto
, jest więc
przeliczalny.
Ponadto
![]() , jest więc przeliczalny na mocy
(2).
, jest więc przeliczalny na mocy
(2).![]()
 , więc zawsze
, więc zawsze
W szczególności jest przeliczalnie wiele wielomianów o współczynnikach wymiernych. Każdy z nich ma skończenie wiele pierwiastków. Pierwiastki takich wielomianów nazywamy liczbami algebraicznymi. Widzimy więc, że jest przeliczalnie wiele liczb algebraicznych. Istnieją również zbiory nieprzeliczalne.
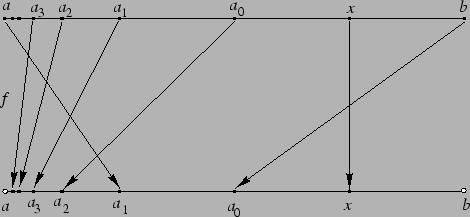
Przypuśćmy nie wprost, że ![]() jest przeliczalny,
tzn. jego elementy można ustawić w ciąg:
jest przeliczalny,
tzn. jego elementy można ustawić w ciąg:
![]() . Zatem
. Zatem ![]() to ciąg wszystkich liczb
rzeczywistych z przedziału
to ciąg wszystkich liczb
rzeczywistych z przedziału ![]() . Sprzeczność osiągniemy
wskazując liczbę rzeczywistą z przedziału
. Sprzeczność osiągniemy
wskazując liczbę rzeczywistą z przedziału ![]() , która nie jest
wyrazem tego ciągu.
, która nie jest
wyrazem tego ciągu.
Każdą z liczb ![]() możemy zapisać w postaci nieskończonego
rozwiniecia dziesiętnego.
możemy zapisać w postaci nieskończonego
rozwiniecia dziesiętnego.

Skoro ![]() jest nieprzeliczalny, a liczb algebraicznych jest
przeliczalnie wiele, to liczb niealgebraicznych (zwanych inaczej
przestępnymi) jest nieprzeliczalnie wiele.
jest nieprzeliczalny, a liczb algebraicznych jest
przeliczalnie wiele, to liczb niealgebraicznych (zwanych inaczej
przestępnymi) jest nieprzeliczalnie wiele.
Ludomir Newelski 2006-08-29