(Przeciw)obrazy, ciągi, działania uogólnione

Załóżmy że $f:X\to Y$. Niech $A,B\subseteq X$ i $C,D\subseteq Y$.

Definicja 10..1 (1)   Obrazem zbioru $A$ względem funkcji $f$ nazywamy zbiór

$$f[A]=\{y\in Y:(\exists x\in A)f(x)=y\},$$

to znaczy zbiór wartości funkcji $f$ dla argumentów ze zbioru $A$.
(2) Przeciwobrazem zbioru $C$ względem funkcji $f$ nazywamy zbiór^10.1

$$f^{-1}[C]=\{x\in X: f(x)\in C\},$$

czyli zbiór tych argumentów, dla których wartość funkcji $f$ należy do zbioru $C$.

Operacje brania obrazu i przeciwobrazu zbioru względem funkcji $f$ mają następujące własności.

1. $f[A\cup B]=f[A]\cup f[B]$
2. $f[A\cap B]\subseteq f[A]\cap f[B]$
3. $f[A]\setminus f[B]\subseteq f[A\setminus B]$
4. $f^{-1}[C\cap D]=f^{-1}[C]\cap f^{-1}[D]$
5. $f^{-1}[C\cup D]=f^{-1}[C]\cup f^{-1}[D]$

W powyższych zdaniach inkluzja na ogół nie może być zastąpiona równością.
Dowód. (1) By pokazać równość zbiorów $f[A\cup B],\ f[A]\cup f[B]$ pokażemy obie inkluzje: $f[A\cup B]\subseteq f[A]\cup f[B]$ i $f[A\cup B]\supseteq f[A]\cup f[B]$.

(a) $\subseteq$. Niech $y\in f[A\cup B]$. Wtedy dla pewnego $x\in A\cup B$ mamy $f(x)=y$. Gdy $x\in A$, to wtedy $y=f(x)\in f[A]$. Gdy $x\in B$, to wtedy $y=f(x)\in f[B]$. W obu przypadkach $y\in f[A]\cup f[B]$.

(b) $\supseteq$. Skoro $A\subseteq A\cup B$, to $f[A]\subseteq f[A\cup B]$. Podobnie dostajemy $f[B]\subseteq f[A\cup B]$. Dlatego $f[A]\cup f[B]\subseteq f[A\cup B]$.

(2) Niech $y\in f[A\cap B]$. Wybieramy $x\in A\cap B$ takie, że $f(x)=y$. Skoro $x\in A$ i $x\in B$, to również $y=f(x)$ należy do obu zbiorów $f[A]$ i $f[B]$, a zatem i do ich przekroju $f[A]\cap f[B]$.

Inkluzji nie możemy zastąpić tu równością. Świadczy o tym następujący przykład. Niech $f:{\mathbb{R}}\to{\mathbb{R}}$ będzie funkcją stale równą $0$, $A=(\infty, 0), B=(0,\infty)$. Wówczas $f[A]=f[B]=\{0\}$, zaś $f[A\cap B]=f[\emptyset]=\emptyset$, więc $f[A\cap B]\neq f[A]\cap f[B]$.

(3) Ćwiczenie.

(4) Niech $x\in X$ będzie dowolne. Korzystając z definicji przeciwobrazu i przekroju zbiorów dostajemy ciąg zdań równoważnych, który dowodzi tezy.

$$x\in f^{-1}[C\cap D]$$

$$\Updownarrow$$

$$f(x)\in C\cap D$$

$$\Updownarrow$$

$$f(x)\in C\land f(x)\in D$$

$$\Updownarrow$$

$$x\in f^{-1}[C]\land x\in f^{-1}[D]$$

$$\Updownarrow$$

$$x\in f^{-1}[C]\cap f^{-1}[D]$$

(5) Podobny dowód. $\Box$

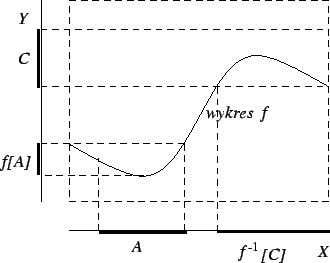
W przypadku, gdy $A\subseteq X\times Y$, zbiór $\pi_X[A]$(rzut zbioru $A$ na pierwszą oś) to po prostu obraz zbioru $A$ względem funkcji $\pi_X$. Podobnie interpretujemy zbiór $\pi_Y[A]$.

Ciągi.

W matematyce pewne szczególne funkcje obdarza się specjalnymi nazwami.

Definicja 10..2   Ciągiem nazywamy dowolną funkcję, której dziedziną jest zbiór liczb naturalnych.

W przypadku ciągów stosujemy też specjalną notację i terminologię. Zapis $(a_n)$ lub $(a_n)_{n\in\mathbb{N}}$ lub $\{a_n\}_{n\in\mathbb{N}}$ oznacza ciąg $f$ taki, że $f(0)=a_0,f(1)=a_1,\dots$

Elementy $a_0,a_1,\dots$ nazywamy wyrazami ciągu $(a_n)$, zaś zapis $(a_n)$ możemy uważać za skrót nieskończonego zapisu $(a_0,a_1,a_2,\dots)$.

Ciąg skończony $k+1$-wyrazowy $\overline{a}=(a_0,a_1,\dots,a_k)$ to funkcja $\overline{a}$ o dziedzinie $\{0,1,2,\dots, k\}$ taka, że $\overline{a}(0)=a_0,\overline{a}(1)=a_1,\dots,\overline{a}(k)=a_k$.

Czasami funkcję $f:X\to Y$ nazywa się ciągiem uogólnionym, traktując zbiór $X$ jako ``zbiór indeksów'' i zapisując $f$ w formie $(a_x)_{x\in X}$. Mamy tu $f(x)=a_x$.

Dla ciągów stosujemy zasadniczo te same definicje, co dla funkcji. Mówimy więc o ciągach różnowartościowych, ``na'' itd. Przykładowo,

$$\mbox{ ciąg }(a_n)\mbox{ jest 1-1 }\Leftrightarrow (\forall n,k\in{\mathbb{N}})(n\neq k\Rightarrow a_n\neq a_k).$$

W przypadku funkcji $f:{\mathbb{R}}\to{\mathbb{R}}$ definiuje się pojęcia funkcji monotonicznych w różnym sensie.

1. $f$ jest rosnąca $\Leftrightarrow(\forall x,y)(x<y\Rightarrow f(x)<f(y))$.
2. $f$ jest słabo rosnąca (niemalejąca) $\Leftrightarrow(\forall x,y)(x<y\Rightarrow f(x)\leq f(y))$.
3. $f$ jest malejąca $\Leftrightarrow(\forall x,y)(x<y\Rightarrow f(x)>f(y))$.
4. $f$ jest słabo malejąca (nierosnąca) $\Leftrightarrow(\forall x,y)(x<y\Rightarrow f(x)\geq f(y))$.

Funkcje mające własności 1. lub 3. nazywamy monotonicznymi, zaś 2. lub 4. słabo monotonicznymi. Te same definicje odnoszą się do ciągów liczb rzeczywistych.

Przy pomocy symboliki logicznej można precyzyjnie zapisać różne własności ciągów czy funkcji.

Niech $(a_n)$ będzie ciągiem liczb rzeczywistych oraz $a\in\mathbb{R}$.

$$\lim_{n\to\infty}a_n=a\Leftrightarrow(\forall\epsilon>0)(\exists n\in {\mathbb{N}})(\forall k>n)\vert a_k-a\vert<\epsilon$$

$$\Leftrightarrow(\forall\epsilon\in{\mathbb{R}})(\exists n\in{... ...\epsilon>0\Rightarrow(k>n\Rightarrow\vert a_k-a\vert<\epsilon))$$

W drugiej wersji kwantyfikatory nie są zrelatywizowane.

$$\mbox{Ciąg }(a_n)\mbox{ jest zbieżny }\Leftrightarrow\exists ... ...rall\epsilon>0)\exists n(\forall k>n)\vert a_k-a\vert<\epsilon.$$

Używając praw de Morgana rachunku kwantyfikatorów dostajemy, że

$$\mbox{ciąg }(a_n)\mbox{ nie jest zbieżny }\Leftrightarrow\for... ...s\epsilon>0)\forall n(\exists k>n)\vert a_k-a\vert\geq\epsilon.$$

Niech $f:{\mathbb{R}}\to{\mathbb{R}}$, $a,b\in\mathbb{R}$. Zgodnie z definicją Cauchy'ego

$$\lim_{x\to a}f(x)=b\Leftrightarrow(\forall\epsilon>0)(\exists... ...l x(\vert x-a\vert<\delta\Rightarrow\vert f(x)-b\vert<\epsilon)$$

$$\Leftrightarrow\forall\epsilon\exists\delta\forall x(\epsilon... ...d(\vert x-a\vert<\delta\Rightarrow\vert f(x)-b\vert<\epsilon)).$$

W drugiej wersji nie ma kwantyfikatorów zrelatywizowanych.

Jako ćwiczenie warto zapisać symbolicznie inne własności ciągów i funkcji rozważane w analizie. Podajemy przykładowo formalizację pewnych typowych zwrotów matematycznych. Niech $\varphi(x),x\in\mathbb{R}$ będzie funkcją zdaniową.

$$\mbox{\lq\lq dla dowolnie dużych $x,\ \varphi(x)$''}\Leftrightarrow\forall y(\exists x>y)\varphi(x)$$

To samo znaczy zdanie ``istnieją dowolnie duże $x$ takie, że $\varphi(x)$''.

$$\varphi(x)\mbox{ zachodzi począwszy od pewnego miejsca }\Leftrightarrow\exists y(\forall x>y)\varphi(x)$$

To samo znaczy zdanie ``dla (wszystkich) dostatecznie dużych $x$ zachodzi $\varphi(x)$''.

Działania uogólnione na zbiorach.

O kwantyfikatorze $\exists$ w zdaniu $(\exists x\in X)\varphi(x)$ możemy myśleć jak o uogólnionej, nieskończonej alternatywie zdań $\varphi(x)$, gdzie $x$ przebiega zakres $X$. Podobnie $\forall$ możemy traktować jak uogólnioną, nieskończoną koniunkcję. W rachunku zbiorów odpowiadają im odpowiednie nieskończone sumy i przekroje.

Niech mianowicie $(A_n)_{n\in\mathbb{N}}$ będzie ciągiem zbiorów. Zbiór wyrazów tego ciągu zapisany w postaci $\{A_n:n\in{\mathbb{N}}\}$ nazywamy też indeksowaną rodziną zbiorów. W tym przypadku nieskończoną sumę

$$A_0\cup A_1\cup A_2\cup\dots$$

zapisujemy jako $\bigcup_{n\in {\mathbb{N}}}A_n$ lub $\bigcup_{n=0}^{\infty} A_n$. Formalnie

$$x\in\bigcup_{n\in {\mathbb{N}}}A_n\Leftrightarrow(\exists n\i... ...n\in {\mathbb{N}}}A_n=\{x:(\exists n\in{\mathbb{N}})x\in A_n\}.$$

Podobnie nieskończony przekrój

$$A_0\cap A_1\cap A_2\cap\dots$$

zapisujemy jako $\bigcap_{n\in {\mathbb{N}}}A_n$ lub $\bigcap_{n=0}^{\infty} A_n$. Formalnie

$$x\in\bigcap_{n\in {\mathbb{N}}}A_n\leftrightarrow(\forall n\i... ...n\in {\mathbb{N}}}A_n=\{x:(\forall n\in{\mathbb{N}})x\in A_n\}.$$

Przykład. Dla $n\in\mathbb{N}$ określamy $A_n$ wzorem $A_n=[0,{1\over n+1})$, zaś $B_n$ wzorem $B_n=(0,1-{1\over n+1}]$. Wtedy ciągi $({1\over n+1})$ i $(1-{1\over n+1})$ są zbieżne do $0$ i $1$ odpowiednio. Widzimy, że

$$\bigcap_nA_n=\bigcap_n\left[0,{1\over n+1}\right)=\{0\}\mbox{ oraz }$$

$$\bigcup_nB_n=\bigcup_n\left(0,1-{1\over n+1}\right]=(0,1).$$

Ogólniej, gdy $(A_t)_{t\in T}$ jest ciągiem uogólnionym zbiorów (innymi słowy, $\{A_t:t\in T\}$ jest indeksowaną rodziną zbiorów), definiujemy uogólnione sumy i przekroje rodziny zbiorów $\{A_t:t\in T\}$ wzorami

$$\bigcup_{t\in T}A_t=\{x:(\exists t\in T)x\in A_t\}\mbox{ i }\bigcap_{t\in T}A_t=\{x:(\forall t\in T)x\in A_t\}.$$

Mamy więc dla wszystkich $x$

$$x\in\bigcup_{t\in T}A_t\Leftrightarrow(\exists t\in T)x\in A_... ...x\in\bigcap_{t\in T}A_t\Leftrightarrow(\forall t\in T)x\in A_t.$$

Rozważa się również rodziny zbiorów indeksowane układami indeksów. Przykładowo rozważmy rodzinę zbiorów $\{A_{n,m}:n,m\in{\mathbb{N}}\}$. Wówczas dla każdego $n\in\mathbb{N}$ możemy zdefiniować zbiór

$$B_n=\bigcup_{m\in\mathbb{N}}A_{n,m}=\{x:(\exists m\in{\mathbb{N}})x\in A_{n,m}\},$$

a następnie zbiór

$$\bigcap_{n\in\mathbb{N}}\bigcup_{m\in\mathbb{N}}A_{n,m}=\bigcap_{n\in\bf N}B_n.$$

Widzimy więc, że

$$x\in \bigcap_{n\in\mathbb{N}}\bigcup_{m\in\bf N}A_{n,m}\Leftr... ...forall n\in{\mathbb{N}})(\exists m\in{\mathbb{N}})x\in A_{n,m}.$$

Podobnie definiujemy zbiory takie, jak $\bigcup_n\bigcap_mA_{n,m}$.

Jeszcze ogólniej, gdy ${\cal A}$ jest rodziną zbiorów, definiujemy sumę i przekrój wszystkich zbiorów z rodziny ${\cal A}$ wzorami

$$\bigcup{\cal A}=\{x:(\exists A\in{\cal A})x\in A\}\mbox{\ \ i\ \ }\bigcap{\cal A}=\{x:(\forall A\in{\cal A})x\in A\}.$$

Mamy więc

$$x\in\bigcup{\cal A}\Leftrightarrow(\exists A\in{\cal A})x\in ... ...x\in\bigcap{\cal A}\Leftrightarrow(\forall A\in{\cal A})x\in A.$$

Definiuje się też uogólnione produkty kartezjańskie:

$$\prod_{n\in\mathbb{N}}A_n=\{(a_n)_{n\in\mathbb{N}}:(\forall n\in{\mathbb{N}})a_n\in A_n\},$$

$$\prod_{t\in T}A_t=\{(a_t)_{t\in T}:(\forall t\in T)a_t\in A_t\}.$$

Istotną analogią ze zwykłymi produktami kartezjańskimi jest tu fakt, że ciąg (uogólniony) $(a_n)$ (lub $(a_t)_{t\in T}$) ``pamięta'' swoją $n$-tą współrzędną $a_n$ (odpowiednio: $t$-tą współrzędną $a_t$). Poniżej podajemy własności tych uogólnionych operacji. W przypadku zwykłych operacji na zbiorach odpowiednie własności $\cup$ i $\cap$ odpowiadały własnościom spójników $\lor$ i $\land$. Tu własności działań uogólnionych odpowiadają własnościom kwantyfikatorów.

Poniżej zakładamy, że odpowiednio indeksowane zbiory są podzbiorami wspólnej przestrzeni $X$.

1. $(\bigcap_nA_n)^c=\bigcup_nA_n^c,\ (\bigcup_nA_n)^c=\bigcap_nA_n^c$
   (prawa de Morgana dla działań uogólnionych)
2. $\bigcup_n\bigcup_m A_{n,m}=\bigcup_m\bigcup_nA_{n,m}$
3. $\bigcap_n\bigcap_m A_{n,m}=\bigcap_m\bigcap_nA_{n,m}$
4. $\bigcup_n\bigcap_mA_{n,m}\subseteq \bigcap_m\bigcup_nA_{n,m}$
5. $\bigcap_n(A_n\cap B_n)=\bigcap_nA_n\cap\bigcap_nB_n$
6. $\bigcup_n(A_n\cup B_n)=\bigcup_nA_n\cup\bigcup_nB_n$
7. $\bigcup_n(A_n\cap B_n)\subseteq\bigcup_nA_n\cap\bigcup_nB_n$
8. $\bigcap_nA_n\cup\bigcap_nB_n\subseteq\bigcap_n(A_n\cup B_n)$
9. Jeśli $(\forall n\in{\mathbb{N}})A_n\subseteq B_n$, to $\bigcup_nA_n\subseteq \bigcup_nB_n$.
10. $\bigcup_nA_n\cap\bigcup_nB_n=\bigcup_n\bigcup_k(A_n\cap B_k)$
11. $\bigcap_nA_n\cup \bigcap_nB_n=\bigcap_n\bigcap_k(A_n\cup B_k)$

Dowód. (1) Dla przykładu udowodnimy pierwszą równość. Korzystając z praw de Morgana dla rachunku kwantyfikatorów, dla każdego $x\in X$ mamy następujący ciąg zdań równoważnych, który uzasadnia żądaną równość.

$$x\in (\bigcap_nA_n)^c$$

$$\Updownarrow$$

$$\neg(x\in\bigcap_nA_n)$$

$$\Updownarrow$$

$$\neg((\forall n\in{\mathbb{N}})x\in A_n)$$

$$\Updownarrow$$

$$(\exists n\in{\mathbb{N}})\neg(x\in A_n)$$

$$\Updownarrow$$

$$(\exists n\in{\mathbb{N}})x\in A_n^c$$

$$\Updownarrow$$

$$x\in\bigcup_nA_n^c$$

Dowody w pozostałych punktach (do punktu 9. włącznie) są analogiczne, korzystają kolejno z odpowiednich tautologii rachunku kwantyfikatorów z rozdziału 7. Dowody punktów 10. i 11. pozostawiamy jako ćwiczenie (jakim tautologiom rachunku kwantyfikatorów one odpowiadają ?). $\Box$

Podobnie jak w przypadku kwantyfikatorów, na mocy własności 2. i 3. zbiory $\bigcup_n\bigcup_mA_{n,m}$ i $\bigcap_n\bigcap_mA_{n,m}$ zapisujemy w postaci $\bigcup_{n,m\in\mathbb{N}}A_{n,m}$ i $\bigcap_{n,m\in\mathbb{N}}A_{n,m}$.

(Przeciw)obrazy i działania uogólnione.

Załóżmy teraz, że zbiory $A_n$ zawierają się w pewnej przestrzeni $X$, zbiory $B_n$ zawierają się w pewnej przestrzeni $Y$ oraz $f:X\to Y$. Operacje brania obrazu i przeciwobrazu względem $f$ mają w tym kontekście następujące własności. Dowody pomijamy.

1. $f[\bigcup_nA_n]=\bigcup_nf[A_n]$
2. $f[\bigcap_nA_n]\subseteq \bigcap_nf[A_n]$
3. $f^{-1}[\bigcup_nB_n]=\bigcup_nf^{-1}[B_n]$
4. $f^{-1}[\bigcap_nB_n]=\bigcap_nf^{-1}[B_n]$